一阶减缩积分与沙漏控制¶

约 2379 个字 4 张图片预计阅读时间 8 分钟

内容声明

本文转载自微信公众号：有限元术。
原文链接：点击查看原文
如有侵权请联系删除，转载请注明出处。

在有限元分析的广阔领域中，准确高效地模拟复杂结构的力学行为是工程师们不懈追求的目标。缩减积分单元是一种重要的单元技术，其可以同时克服剪切自锁和体积自锁两个方面的自锁现象，同时一些情况下采用缩减积分计算效率也相比全积分单元高，因此在有限元软件中得以广泛的应用。

在知名有限元软件Abaqus中，三维8节点六面体单元默认的单元类型就是三维八节点六面体缩减积分单元C3D8R。

今天，我们就一同深入探索 C3D8R 单元的缩减积分奥秘以及至关重要的沙漏控制技术，本文主要包括以下内容：

C3D8R 单元简介
减缩积分原理
沙漏现象产生机制
沙漏现象控制方法
1. 细化网格
2. 避免集中荷载
3. 设置沙漏控制选项

1 C3D8R 单元简介¶

C3D8R 单元

“C” 代表连续体（Continuum），“3D” 明确其为三维单元，“8” 表示具有八个节点，“R” 则是 Reduced 的缩写，意味着该单元采用了缩减积分方法

与完全积分单元相比，C3D8R 单元在每个方向上少用一个积分点，线性减缩积分的它仅在单元中心包含一个积分点。这一独特的积分方式赋予了 C3D8R 单元诸多优势。

优势：

在弯曲荷载作用下，C3D8R 单元不易发生剪切自锁现象，能更准确地求解位移结果
即便网格存在一定程度的扭曲变形，其分析精度也不会受到太大影响

缺点：

由于只有单元中心一个积分点，在应力集中部位，经过插值和平均后得到的节点应力并不精确，不适用于以节点应力为关键指标的分析
为了克服其特有的沙漏问题，往往需要划分较细的网格，这在一定程度上增加了计算成本和工作量。

2 减缩积分原理¶

积分在有限元分析中起着将单元内的物理量（如应力、应变）从局部积分点的值扩展到整个单元的关键作用。

完全积分单元

每个方向上布置多个积分点（例如 C3D8 单元在每个方向有 2 个高斯积分点，总共2x2x2 个积分点），能够较为精确地对单元内的各种物理量进行积分计算

缩减积分单元

以 C3D8R 为代表，为了降低计算量，在每个方向减少一个积分点，C3D8R仅在单元中心设置一个积分点，C3D20R共8个积分点

这种方式在很多情况下能够有效避免使用完全积分产生的刚度过大、应力不连续等问题，大大提高了计算效率，使得在处理大规模复杂模型时成为可能。但同时，缩减积分也带来了一个棘手的问题 —— 沙漏现象。

一般情况下一阶单元的缩减积分实际上至少有两种方式可以实现：

一种是直接采用单个积分点计算应变和B矩阵，即 计算单元中心点的应变和B矩阵：

\[ B^I_{i}=N^I_{i}(0,0,0) \]

另一种是 通过“均匀应变格式”计算应变和B矩阵：

\[ B _ { i } ^ { I } = \frac { 1 } { V _ { e \ell } } \int _ { V _ { e \ell } } N _ { i } ^ { I } ( g , h , r ) \, d V _ { e \ell } \]

Tip

在Abaqus/explicit中，可以选择以上的任意一种方式来实现单点积分
在Abaqus/implicit中，使用的是第二种方式

3 沙漏现象产生机制¶

沙漏模式是一种非物理的 零能变形模式，形象地说，就是单元发生了变形，然而却没有对应的应力或应变产生。这一现象主要出现在像 CPS4R、CAX4R、C3D8R 等线性减缩积分单元的应力/位移场分析中。

由于线性单元本身积分点数目较少，减缩积分又进一步减少了积分点，当单元受到弯曲或剪切作用时，可能会出现一种特殊情况：虽然节点位移显示单元发生了形变，但通过插值得到的应变却为零。

实际上，沙漏产生的真正原因在于使用缩减积分计算出的 刚度矩阵是“缺秩”的，即计算得到的单元刚度矩阵的秩比实际应当具备的矩阵秩小，所以如果不进行沙漏控制，是无法求解得到准确结果的。

C3D8R 单元

一共有24个自由度，对于整个单元去掉6个刚体位移自由度后，刚度矩阵应当还具备18个自由度，而采用单点积分的刚度矩阵仅为6。

沙漏控制，正是对刚度矩阵进行修正，在单点积分的刚度矩阵的基础上加上沙漏刚度，从而获得可以求解的刚度矩阵。

当网格较粗时，对于：

一阶单元C3D8R，沙漏现象会通过网格不断扩展，使得计算结果变得毫无意义，甚至可能导致严重的网格畸变，使整个有限元分析的准确性大打折扣，因此需要进行沙漏控制
二阶单元C3D20R，Abaqus认为其沙漏通常不会严重扩散，因此Abaqus没有对其进行沙漏控制。

4 沙漏现象控制方法¶

4.1 细化网格¶

这是一种直观且有效的方法。当使用线性减缩积分单元时，避免划分过于粗糙的网格至关重要。尤其是在结构可能发生弯曲变形的部位， 在厚度方向应至少划分 4 个单元。

通过细化网格，能够有效减少沙漏模式在单元间传播的可能性，使得每个单元的变形更加合理，从而降低沙漏现象对整体计算结果的影响。

但细化网格也并非毫无代价，它会显著增加计算量和计算时间，对计算机硬件性能提出更高要求。

4.2 避免集中荷载¶

将载荷或边界条件只定义在一个节点上，容易引发沙漏模式的扩展。因此，我们应尽量将点载荷或点上的边界条件定义在一个包含 该点的小区域上。

这样做有利于避免沙漏模式的产生，使得载荷的传递更加均匀合理，减少因局部异常受力导致的沙漏现象。

在实际建模过程中，这需要工程师们对模型的受力情况进行细致分析，合理设置载荷和边界条件的施加方式。

通过绘制伪应变能 ALLAE（artificial strain energy）和内能 ALLIE（internal energy）的曲线，我们可以清晰地判断沙漏模式对计算结果的影响程度。

Check

伪应变能 ALLAE 约占内能 ALLIE 的 1% 时，表明沙漏模式对计算结果的影响较小
伪应变能超过总内能的 10% 时，分析结果基本无效，必须采取措施加以解决

4.3 设置沙漏控制选项¶

Abaqus 等有限元软件为线性减缩积分单元提供了多种沙漏控制选项。其核心思路是引入少量的人工 “沙漏刚度”，以此来限制沙漏模式的扩展。

在 Abaqus 的 Mesh 功能模块中选用线性减缩积分单元时，可以选择 Enhanced 、 Relax stiffness 、 Stiffness 等沙漏刚度控制方式。

这些方式通过巧妙地调整单元的刚度矩阵，为单元增加一定抵抗沙漏变形的能力。当网格足够细化时，配合合适的沙漏控制选项，能够获得足够精确的计算结果。

然而，设置沙漏控制参数需要一定的经验和技巧，参数设置不当可能无法有效抑制沙漏现象，或者引入过多的人工刚度，同样影响计算精度。

关于沙漏刚度的具体计算方法，这里给出Abaqus中选用“Stiffness”时（这也是默认的方式）的公式：

\[ Q = s ^ { s } ( ( r _ { F } G ) \, B _ { \alpha } ^ { P } { B } _ { \alpha } ^ { P } \, V ) q \]

这里\(Q\)和\(q\)分别是沙漏广义力和对应的沙漏模态，通过对上式进行变分，即可得到沙漏刚度的表达式。

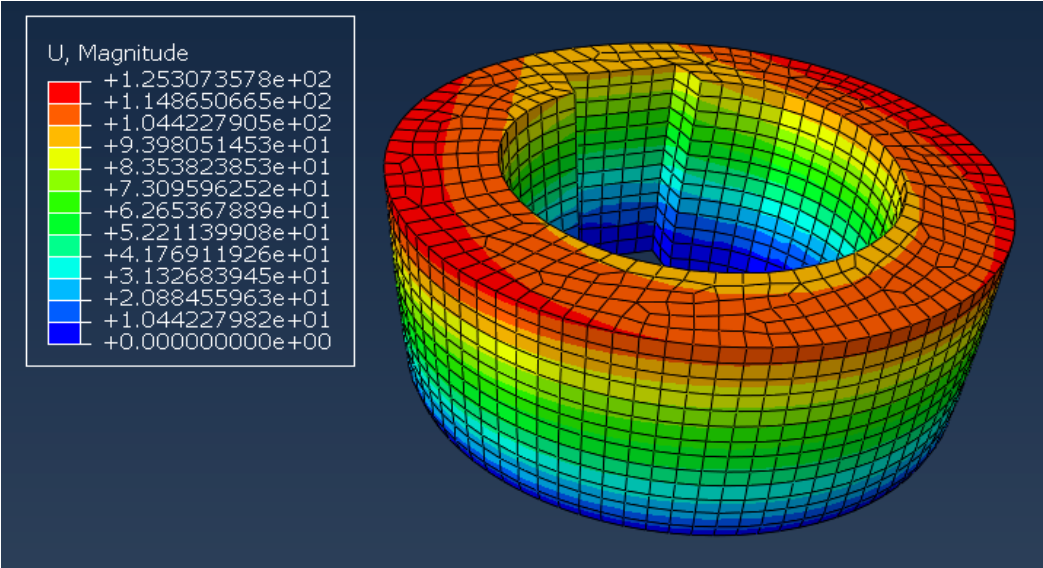
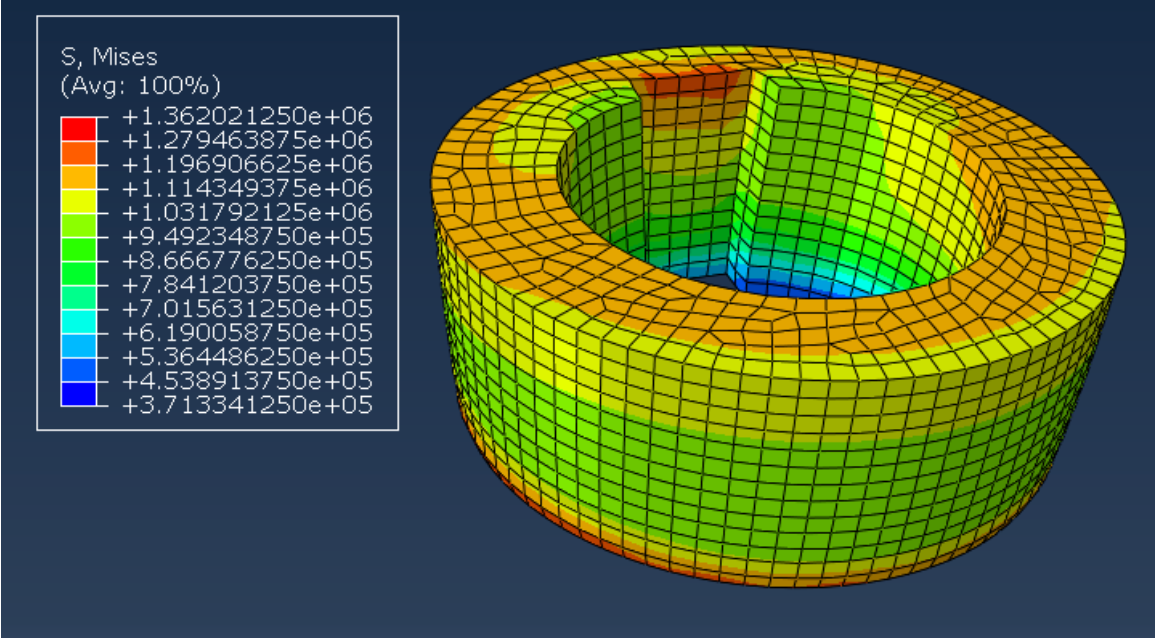
在本公众号(有限元术)开发的有限元求解器Hanfem中，依据上述理论采用C3D8R的计算结果与Abaqus对比如下：

C3D8R 单元的缩减积分技术在提高有限元分析计算效率方面功不可没，而沙漏控制则是确保其计算精度的关键所在。

工程师们在实际应用中，需要根据具体问题的特点，综合运用各种沙漏控制方法，精心设置相关参数，合理划分网格，才能充分发挥 C3D8R 单元的优势，得到准确、高效的有限元分析结果。