Mesh2D:inpoly¶
约 608 个字 217 行代码 9 张图片 预计阅读时间 5 分钟
本期给大家带来的是 Mesh2D 项目中的 inpoly 方法,该方法与 matlab 内置的 inpolygon 方法相似,用于判定一组点是否在任意二维多边形内部,在判定的过程中效率相当高,尤其是边界复杂的情况下,优势越明显。
主要功能¶
INPOLY 用于判断一组点(VERT)是否在任意二维多边形(PSLG)内部。它支持一般的非凸和多连通(带洞)多边形。
Note
- INPOLY 基于“穿越数(crossing-number)”测试:
- 具体做法是,从每个点向右引一条射线,统计它与多边形边界的交点个数。如果交点数是奇数,则点在多边形内,否则在外部
- 朴素做法需要每个点和每条边都判断一遍,复杂度 O(N*M),速度较慢(N 为测试点数,M 为多边形边数)
- INPOLY 的优化:
- 先按 y 值排序点,通过二分法快速锁定可能交点的边
- 这样大幅减少了实际需要判定的边数
- 平均复杂度可达到 O((N+M)*LOG(N)),非常快
案例一: 基础操作¶
几何区域¶
node = [
4,0 % 外环
8,4
4,8
0,4
3,3 % 内洞
5,3
5,5
3,5
];
edge = [
1,2 % 外环
2,3
3,4
4,1
5,6 % 内洞
6,7
7,8
8,5
];
整个区域生成点组¶
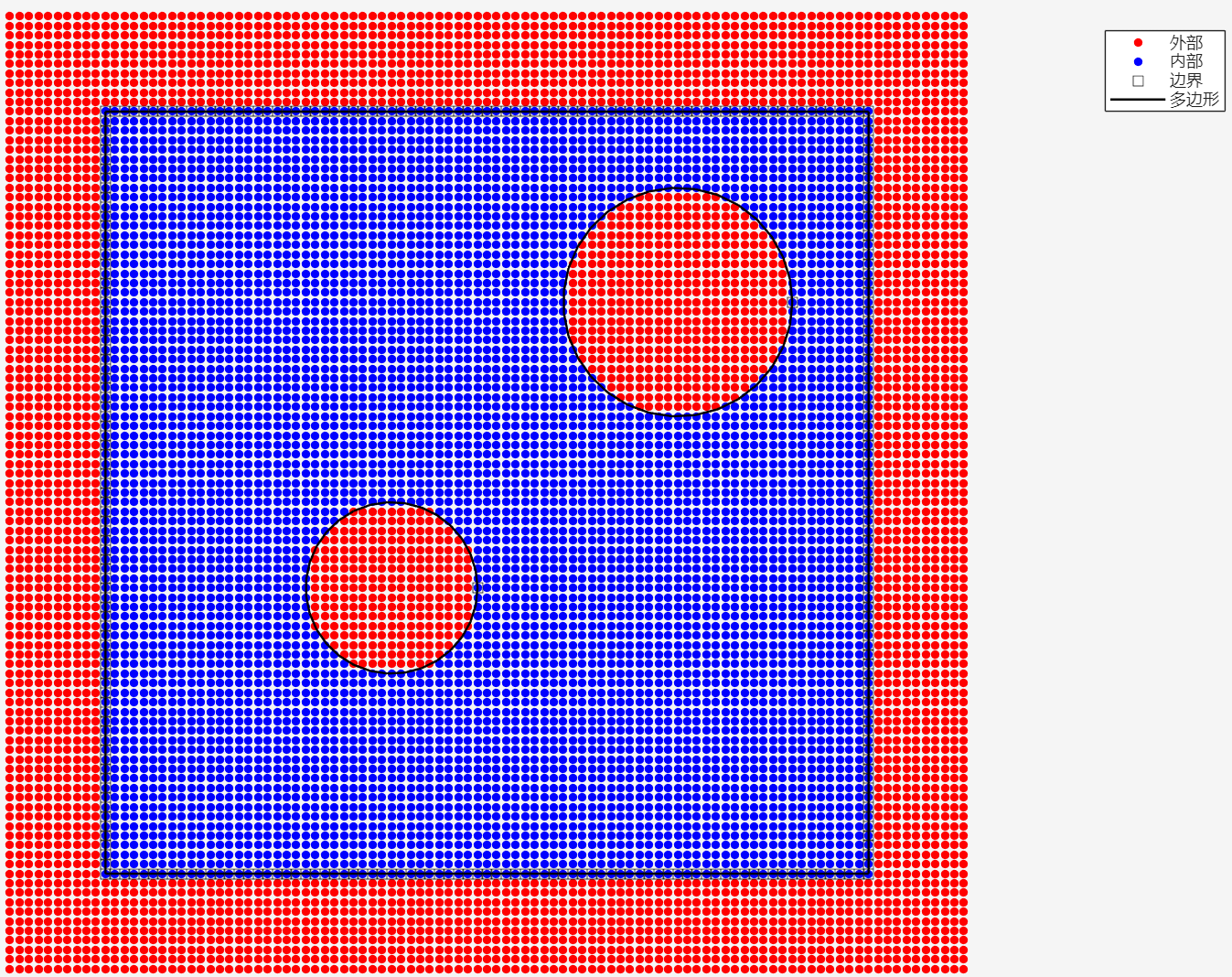
判断点的位置¶
- stat:逻辑数组 \([2601\times1]\),值为 1 的点表示内部和边界的点
- bnds:逻辑数组 \([2601\times1]\),值为 1 的点表示边界上的点
可视化¶
figure; hold on; axis equal off;
plot(xpos(~stat), ypos(~stat), 'r.', 'markersize', 14); % 外部
plot(xpos(stat), ypos(stat), 'b.', 'markersize', 14); % 内部
plot(xpos(bnds), ypos(bnds), 'ks', 'markersize', 7); % 边界点
% ------ 画多边形所有边 ------
for i = 1:size(edge,1)
plot(node(edge(i,:),1), node(edge(i,:),2), 'k-', 'LineWidth', 1.2);
end
legend('外部','内部','边界','多边形','Location','northeast');
案例二: 凹多边形¶
几何区域¶
theta = linspace(0, 2*pi, 11)';
R = [4 1 4 1 4 1 4 1 4 1 4]'; % 交替大半径小半径
node = [R.*cos(theta), R.*sin(theta)];
edge = [ (1:10)' (2:11)']; % 顺次连接
edge(end,2) = 1;
[xpos,ypos] = meshgrid(-4:0.1:4);
xpos = xpos(:); ypos = ypos(:);
案例三: 带多个洞的多边形¶
几何区域¶
% 外环(正方形)
node = [0 0; 8 0; 8 8; 0 8];
edge = [1 2;2 3;3 4;4 1];
% 洞1(圆形近似,顺序逆时针)
t = linspace(0,2*pi,32)';
c1 = [3 3] + 0.9*[cos(t), sin(t)];
node = [node; c1];
idx1 = (5:36)';
edge = [edge; [idx1 [idx1(2:end);idx1(1)]]];
% 洞2
c2 = [6 6] + 1.2*[cos(t), sin(t)];
node = [node; c2];
idx2 = (37:68)';
edge = [edge; [idx2 [idx2(2:end);idx2(1)]]];
[xpos,ypos] = meshgrid(-1:0.1:9);
xpos = xpos(:); ypos = ypos(:);
案例四: 带自交的多边形¶
几何区域¶
node = [0 0; 4 8; 8 0; 0 6; 8 6];
edge = [1 2; 2 3; 3 4; 4 5; 5 1];
[xpos,ypos] = meshgrid(-1:0.1:9);
xpos = xpos(:); ypos = ypos(:);
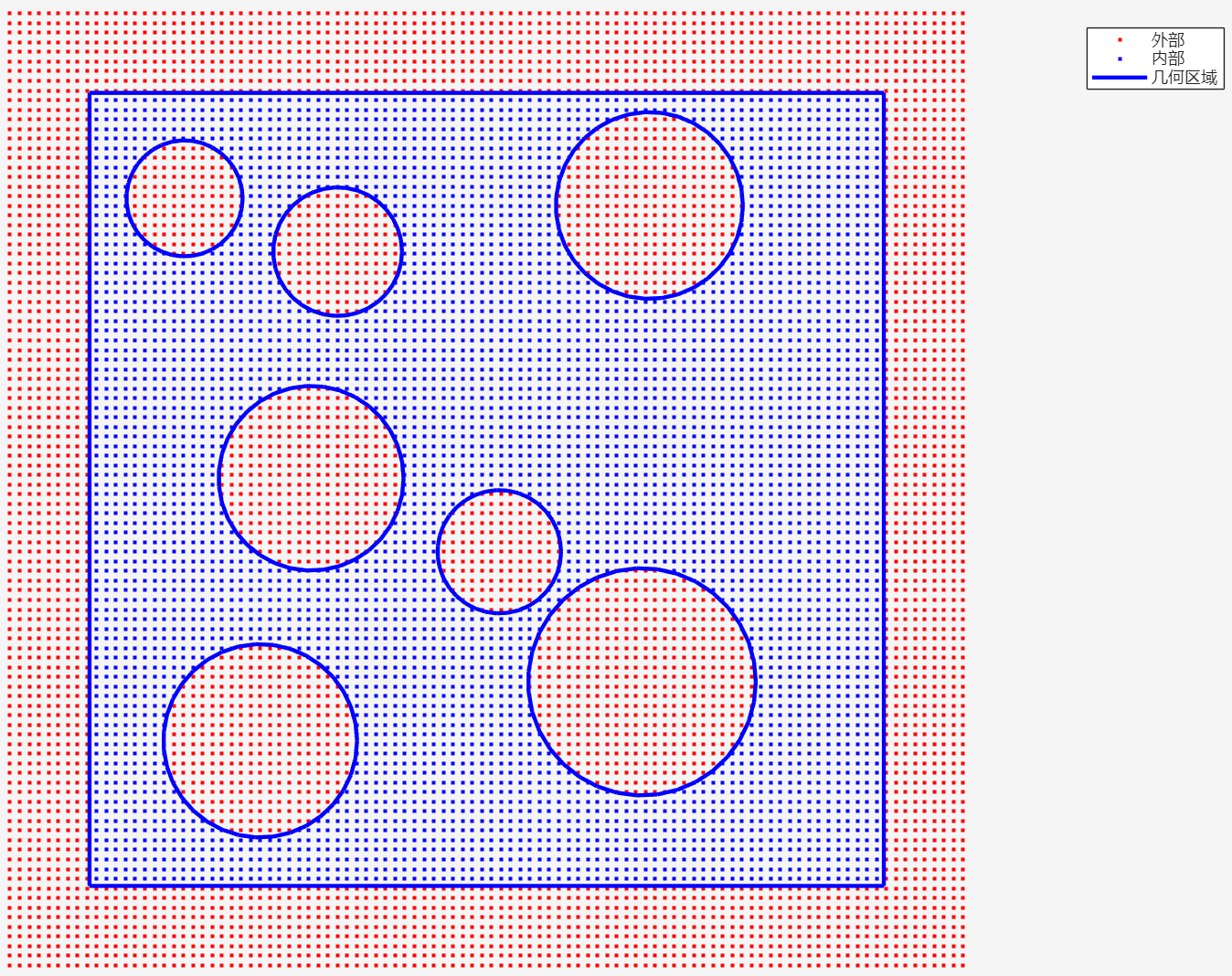
案例五:内部随机孔洞¶
几何区域¶
%% 1. 外环(正方形顺时针)
node = [0 0; 10 0; 10 10; 0 10];
edge = [1 2;2 3;3 4;4 1];
%% 2. 随机生成若干不重叠圆洞
n_hole = 7; % 洞的数量
R_min = 0.7; R_max = 1.5; % 半径范围
hole_centers = [];
hole_radii = [];
theta = linspace(0,2*pi,36)'; % 圆多边形分辨率
% 循环随机放置不重叠圆洞
max_try = 1000; try_cnt = 0;
while size(hole_centers,1) < n_hole && try_cnt < max_try
try_cnt = try_cnt + 1;
r = R_min + (R_max-R_min)*rand;
x = 1.2*r + (10-2.4*r)*rand; % 保证不出界
y = 1.2*r + (10-2.4*r)*rand;
c_new = [x, y];
% 检查是否与已有洞重叠
if isempty(hole_centers)
overlap = false;
else
d = sqrt(sum((hole_centers - c_new).^2,2));
overlap = any(d < (hole_radii + r)*1.05); % 1.05避免浮点误差
end
% 检查是否出界(离外环足够远)
if x-r<0 || x+r>10 || y-r<0 || y+r>10
continue;
end
if ~overlap
hole_centers = [hole_centers; c_new];
hole_radii = [hole_radii; r];
end
end
% 生成所有洞的节点与边
for k = 1:n_hole
c = hole_centers(k,:);
r = hole_radii(k);
circ = c + r*[cos(theta), sin(theta)];
idx0 = size(node,1)+1;
node = [node; circ];
idx = (idx0:(idx0+length(theta)-1))';
edge = [edge; [idx [idx(2:end); idx(1)]]];
end
%% 3. 生成点
[xpos, ypos] = meshgrid(linspace(-1,11,100), linspace(-1,11,100));
xpos = xpos(:);
ypos = ypos(:);
[stat, bnds] = inpoly2([xpos, ypos], node, edge);
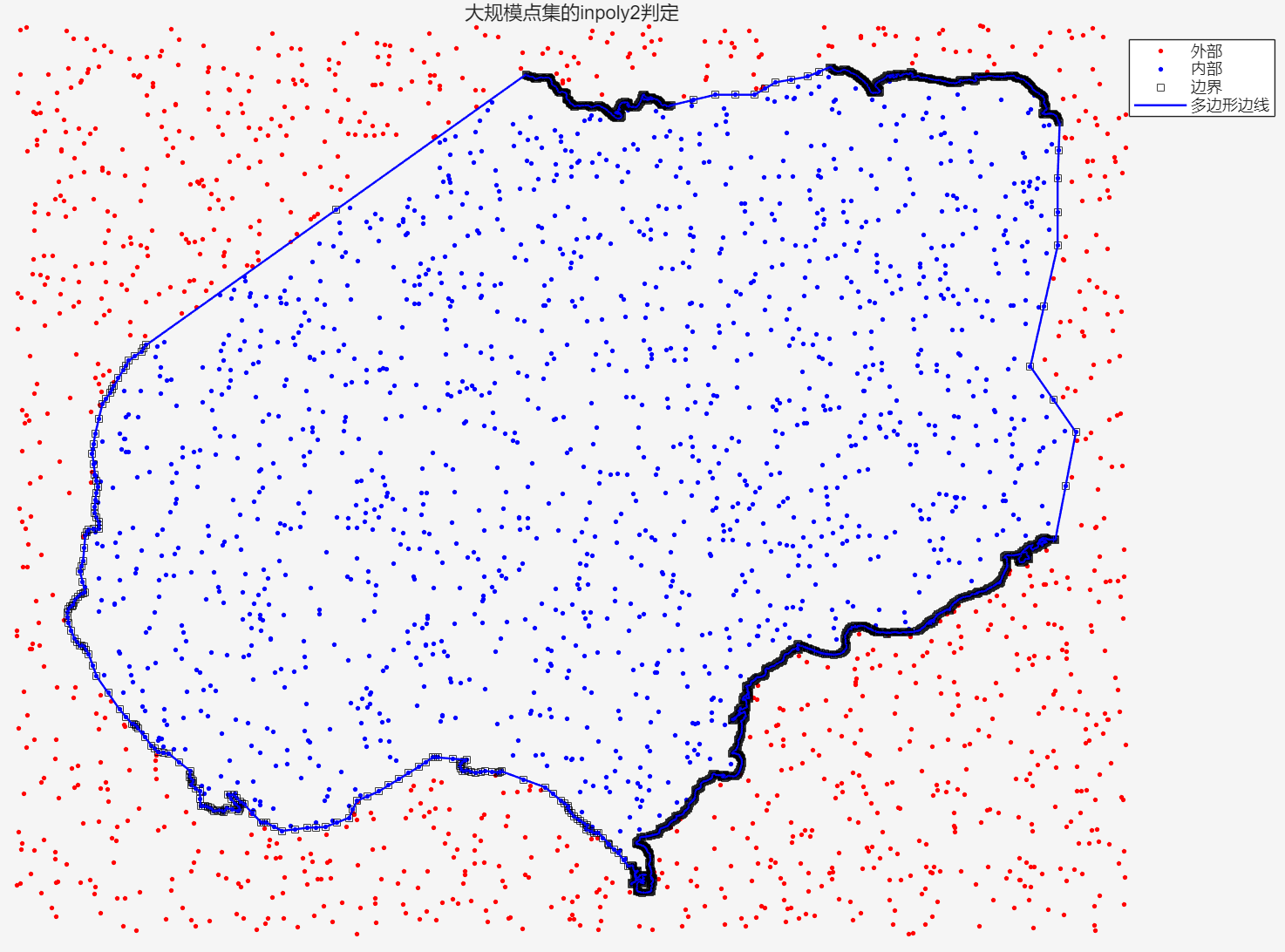
案例六:复杂几何区域¶
对于较为复杂的几何区域,将 inpoly2 与 matlab 内置的inpolygon 进行对比:
clc; clear; close all;
geom = loadmsh('test-data/coast.msh'); % 这里是官方例子
node = geom.point.coord(:,1:2);
edge = geom.edge2.index(:,1:2);
% 随机点密集布满多边形范围
n_rand = 2500;
half = max(node,[],1) + min(node,[],1);
half = half * 0.5;
scal = max(node,[],1) - min(node,[],1);
rpts = rand(n_rand,2);
rpts(:,1) = 1.10*scal(1)*(rpts(:,1)-.5)+half(1);
rpts(:,2) = 1.10*scal(2)*(rpts(:,2)-.5)+half(2);
% 加上所有节点和所有边中点
emid = .5 * node(edge(:,1),:) + .5 * node(edge(:,2),:);
xpos = [node(:,1); emid(:,1); rpts(:,1)];
ypos = [node(:,2); emid(:,2); rpts(:,2)];
tic
[stat, bnds] = inpoly2([xpos, ypos], node, edge);
fprintf('Runtime: %f (INPOLY2)\n', toc);
tic
[stat2, bnds2] = inpolygon(xpos, ypos, node(:,1), node(:,2));
fprintf('Runtime: %f (INPOLYGON)\n', toc);
figure; hold on; axis equal off;
plot(xpos(~stat), ypos(~stat), 'r.', 'markersize', 8);
plot(xpos(stat), ypos(stat), 'b.', 'markersize', 8);
plot(xpos(bnds), ypos(bnds), 'ks', 'markersize', 5);
for i = 1:size(edge,1)
plot(node(edge(i,:),1), node(edge(i,:),2), 'b-', 'LineWidth', 1.2);
end
legend('外部','内部','边界','多边形边线');
title('大规模点集的inpoly2判定');
时间对比结果:
从上面结果来看,inpoly2 比 matlab 内置的 INPOLYGON 方法快了 400 多倍!
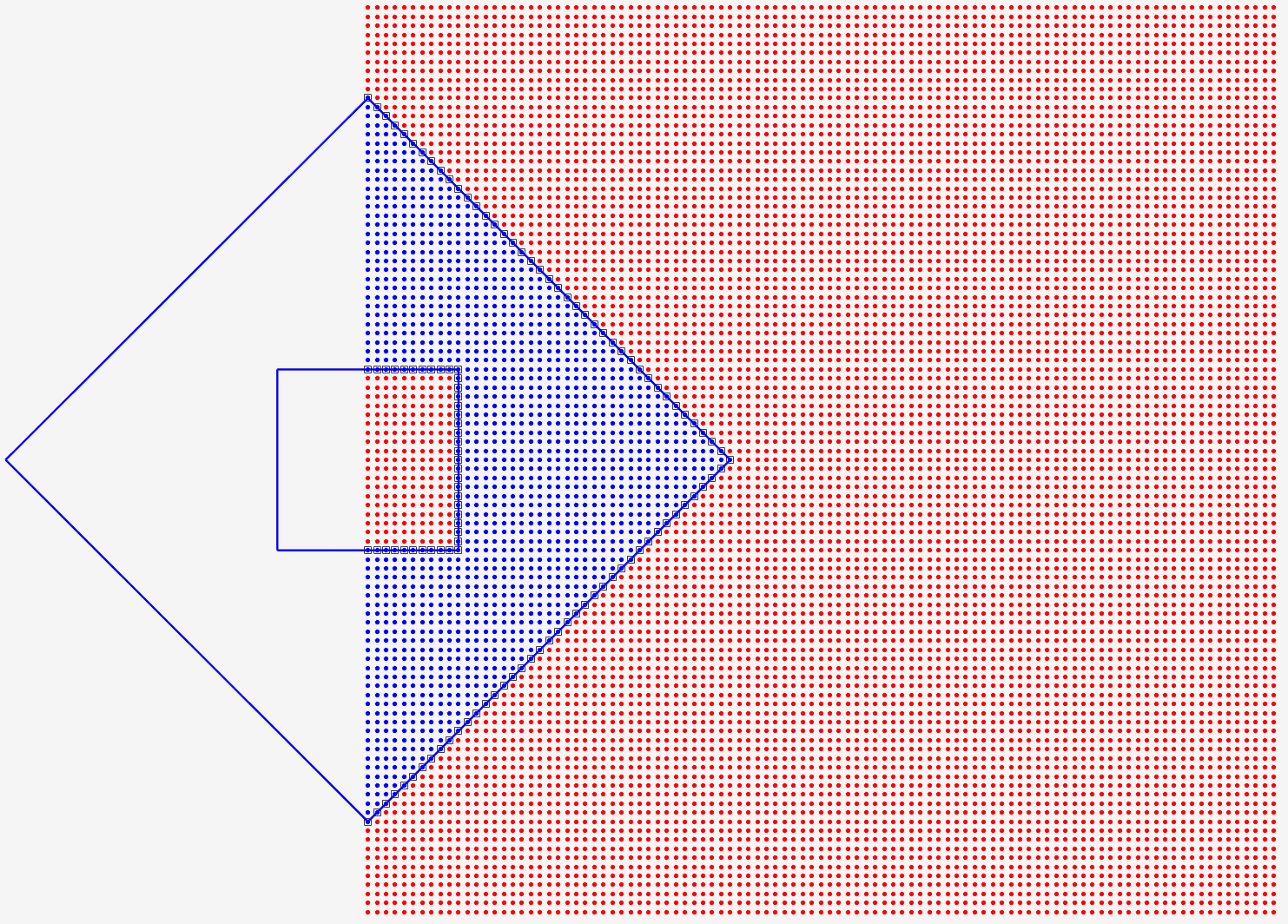
案例七:“空”的情况¶
将案例一的点组向右平移 12,将会得到所有的点都判定为外部的点,算法在极端情况下不会出错。
将案例一的点组向右平移 5,也可以精准判定点的范围。
案例八:边界边缘带¶
inpoly2不传入 edge 信息,空着,第四个参数传入边界边缘带的宽度,返回的on就可以是整个边界边缘带的点了,即距离边界小于 0.01 的点都视为边界点。
完整代码:
clc; close all;
px=[+0.0 -1.0 +0.5 +2.0 +3.0 +0.0]';
py=[-3.0 +1.0 +2.0 +3.0 +2.0 -3.0]';
dx=0.1;
x=linspace(min(px)-dx,max(px)+dx,100);
y=linspace(min(py)-dx,max(py)+dx,100);
[x,y]=meshgrid(x,y);
x=x(:);
y=y(:);
% 可视化多边形
figure; hold on; axis equal off;
plot(px,py,'b-','linewidth',4); % 多边形边
% 先画全部点为红色(外部点的底色)
h_out = plot(x, y, 'r.', 'markersize', 6);
% 调用 inpoly2 判定
[in, on] = inpoly2([x, y], [px, py], [], 1e-2);
in2 = in & ~on; % 纯内部点
% 画内部点(蓝色圆点,覆盖红色点)
h_in = plot(x(in2), y(in2), 'bo', 'markersize', 5, 'MarkerFaceColor', 'b');
% 画边界点(蓝色方块,覆盖红色点)
h_bd = plot(x(on), y(on), 'ks', 'markersize', 7, 'MarkerFaceColor', 'cyan');
legend([h_out h_in h_bd], {'外部点','内部点','边界点'}, 'Location','northeast');
% ---- 选择要放大的局部区域 ----
xrange = [1.0 2.0];
yrange = [1.8 2.8];
% 主图上画放大区域框
rectangle('Position', [xrange(1), yrange(1), diff(xrange), diff(yrange)], ...
'EdgeColor', [1 0.5 0], 'LineWidth', 2, 'LineStyle', '--');
% ---- 添加 inset axes(放大图)----
ax1 = gca; % 主图句柄
ax2 = axes('Position',[0.6 0.58 0.27 0.27]); % [left bottom width height],可调位置和大小
box on; hold on; axis equal;
% 放大图内容与主图一致,但只画局部
plot(px,py,'b-','linewidth',4);
plot(px,py,'bo','markersize',10);
plot(x(~in), y(~in), 'r.', 'markersize', 4);
plot(x(in2), y(in2), 'bo', 'markersize', 4, 'MarkerFaceColor', 'b');
plot(x(on), y(on), 'ks', 'markersize', 6, 'MarkerFaceColor', 'cyan');
set(gca,'XLim',xrange,'YLim',yrange);
set(gca,'xtick',[],'ytick',[]); % 关闭放大图刻度
title('边界细节');
参考文献¶
[1] - J. Kepner, D. Engwirda, V. Gadepally, C. Hill, T. Kraska, M. Jones, A. Kipf, L. Milechin, N. Vembar: Fast Mapping onto Census Blocks, IEEE HPEC, 2020.