Mesh2D：基础操作¶

约 440 个字 105 行代码 3 张图片预计阅读时间 3 分钟

本期开始带着大家学习开源项目 Mesh2D。它是一个基于 MATLAB 的二维 Delaunay 网格生成器（mesh-generator），专门为通用二维几何体生成高质量的 非结构化三角形网格 。其核心用途和特点包括：

可以对各种已知边界信息，进行Delaunay 三角剖分，输出高质量、几何和拓扑优化的二维三角形网格
实现了 Delaunay-refinement 和 Frontal-Delaunay 两种三角剖分技术
内部包含各种网格优化算法
支持自定义网格密度函数，实现不同区域的自适应加密
支持多分区的复合区域网格剖分

基础操作¶

先来操作一下，简单的几何区域及网格参数设置：

定义几何区域¶

node = [ 
    0, 0; 9, 0; 9, 9; 0, 9;  % 外部
    4, 4; 5, 4; 5, 5; 4, 5   % 内部孔
];
edge = [
    1, 2; 2, 3; 3, 4; 4, 1;  % 外部
    5, 6; 6, 7; 7, 8; 8, 5   % 内部
];

调用 refine2 进行网格划分¶

[vert, etri, tria, tnum] = refine2(node, edge);

Tip

vert：新生成节点坐标
tria：三角单元节点索引
etri：有边界约束的边，记录网格所有重要边（边界/内部边）的起止节点编号
tnum：区域编号（域分组号），标记每个三角形属于哪个物理区域（单区域时全为1）

绘图¶

绘制原始边界和新生成的mesh

patch('faces', tria(:,1:3), 'vertices', vert, ...
      'facecolor', 'w', 'edgecolor', [.2,.2,.2]);
hold on; axis image off;
patch('faces', edge(:,1:2), 'vertices', node, ...
      'facecolor', 'w', 'edgecolor', [.1,.1,.1], 'linewidth', 1.5);

调节网格密度参数¶

hfun 控制单元边长，作为输入参数的 第五个位置，目前为常数，后续自定义密度函数时在做详细介绍。

hfun = 0.3; % 变小则更密，变大则更粗
[vert, etri, tria, tnum] = refine2(node, edge, [], [], hfun);

完整代码¶

node = [ 
    0, 0; 9, 0; 9, 9; 0, 9;  % 外部
    4, 4; 5, 4; 5, 5; 4, 5   % 内部孔
];
edge = [
    1, 2; 2, 3; 3, 4; 4, 1;  % 外部
    5, 6; 6, 7; 7, 8; 8, 5   % 内部
];

figure;
subplot(1,2,1)
[vert, etri, tria, tnum] = refine2(node, edge);
patch('faces', tria(:,1:3), 'vertices', vert, ...
      'facecolor', 'w', 'edgecolor', [.2,.2,.2]);
hold on; axis image off;
patch('faces', edge(:,1:2), 'vertices', node, ...
      'facecolor', 'w', 'edgecolor', [.1,.1,.1], 'linewidth', 1.5);
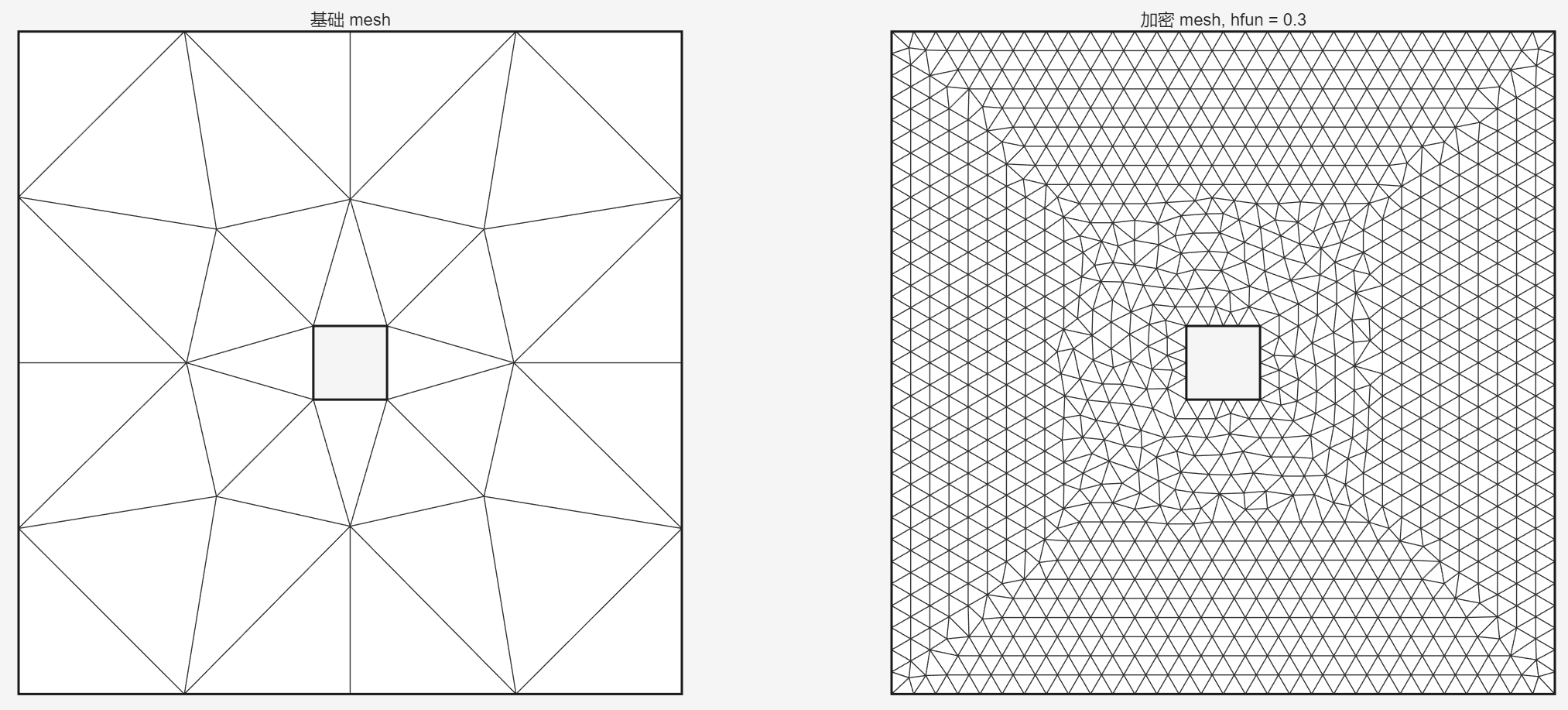
title('基础 mesh');

subplot(1,2,2)
hfun = 0.3;
[vert, etri, tria, tnum] = refine2(node, edge, [], [], hfun);
patch('faces', tria(:,1:3), 'vertices', vert, ...
      'facecolor', 'w', 'edgecolor', [.2,.2,.2]);
hold on; axis image off;
patch('faces', edge(:,1:2), 'vertices', node, ...
      'facecolor', 'w', 'edgecolor', [.1,.1,.1], 'linewidth', 1.5);
title(['加密 mesh, hfun = ', num2str(hfun)]);

进一步学习¶

经过上面案例的学习，是不是对基础的网格划分方法有了一定的认识，现在我们再来试试变换一下几何区域：

圆形内孔¶

完整代码网格形态

% **** 外正方形节点和边 ****
node = [0 0; 9 0; 9 9; 0 9];
edge = [1 2; 2 3; 3 4; 4 1];

% **** 圆孔节点和边 ****
N = 32;        % 圆孔离散点数，越多越圆滑
r = 1;         % 圆半径
cx = 4.5; cy = 4.5;  % 圆心

theta = linspace(0, 2*pi, N+1)';
theta(end) = []; % 去除最后一个和第一个重合
circle_nodes = [cx + r*cos(theta), cy + r*sin(theta)];
circle_edges = [(1:N)' [2:N 1]']; % 连环相接

% **** 拼接 ****
node = [node; circle_nodes];
edge = [edge; (4+(1:N))' (4+[2:N 1])'];

% **** mesh 生成 ****
hfun = 0.25; % 可以试试 0.1, 0.5
[vert, etri, tria, tnum] = refine2(node, edge, [], [], hfun);

figure;
patch('faces', tria(:,1:3), 'vertices', vert, ...
      'facecolor', 'w', 'edgecolor', [.2,.2,.2]);
hold on; axis image off;
patch('faces', edge(:,1:2), 'vertices', node, ...
      'facecolor', 'w', 'edgecolor', 'r', 'linewidth', 1.2);
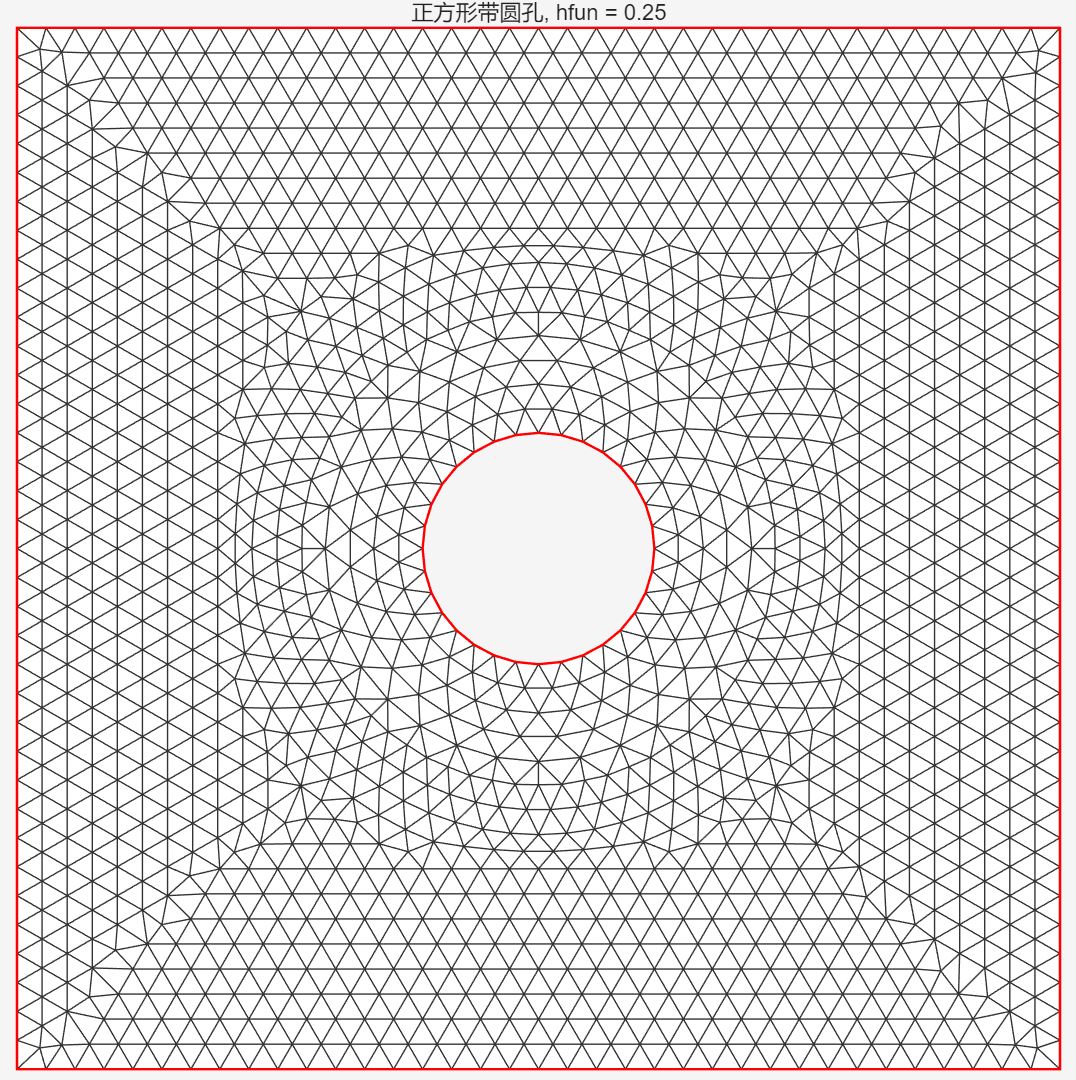
title(['正方形带圆孔, hfun = ', num2str(hfun)]);

几何区域内部多个小孔¶

完整代码网格形态

% **** 外正方形 ****
node = [0,0; 9,0; 9,9; 0,9];

% **** 添加两个圆孔 ****
N = 24;
r = 0.8;
theta = linspace(0, 2*pi, N+1)';
theta(end) = [];

% 孔1
c1 = [2.5 2.5];
circ1 = c1 + r*[cos(theta) sin(theta)];
% 孔2
c2 = [6.5 6.5];
circ2 = c2 + r*[cos(theta) sin(theta)];

node = [node; circ1; circ2];
edge = [1 2; 2 3; 3 4; 4 1; ...           % 外部
(4+(1:N))' (4+[2:N 1])'; ...          % 孔1
(4+N+(1:N))' (4+N+[2:N 1])'];         % 孔2

hfun = 0.22;
[vert, etri, tria, tnum] = refine2(node, edge, [], [], hfun);

figure;
set(gcf,'color','white');
patch('faces', tria(:,1:3), 'vertices', vert, ...
      'facecolor', 'w', 'edgecolor', [.2,.2,.2]);
hold on; axis image off;
patch('faces', edge(:,1:2), 'vertices', node, ...
      'facecolor', 'w', 'edgecolor', 'm', 'linewidth', 1.2);
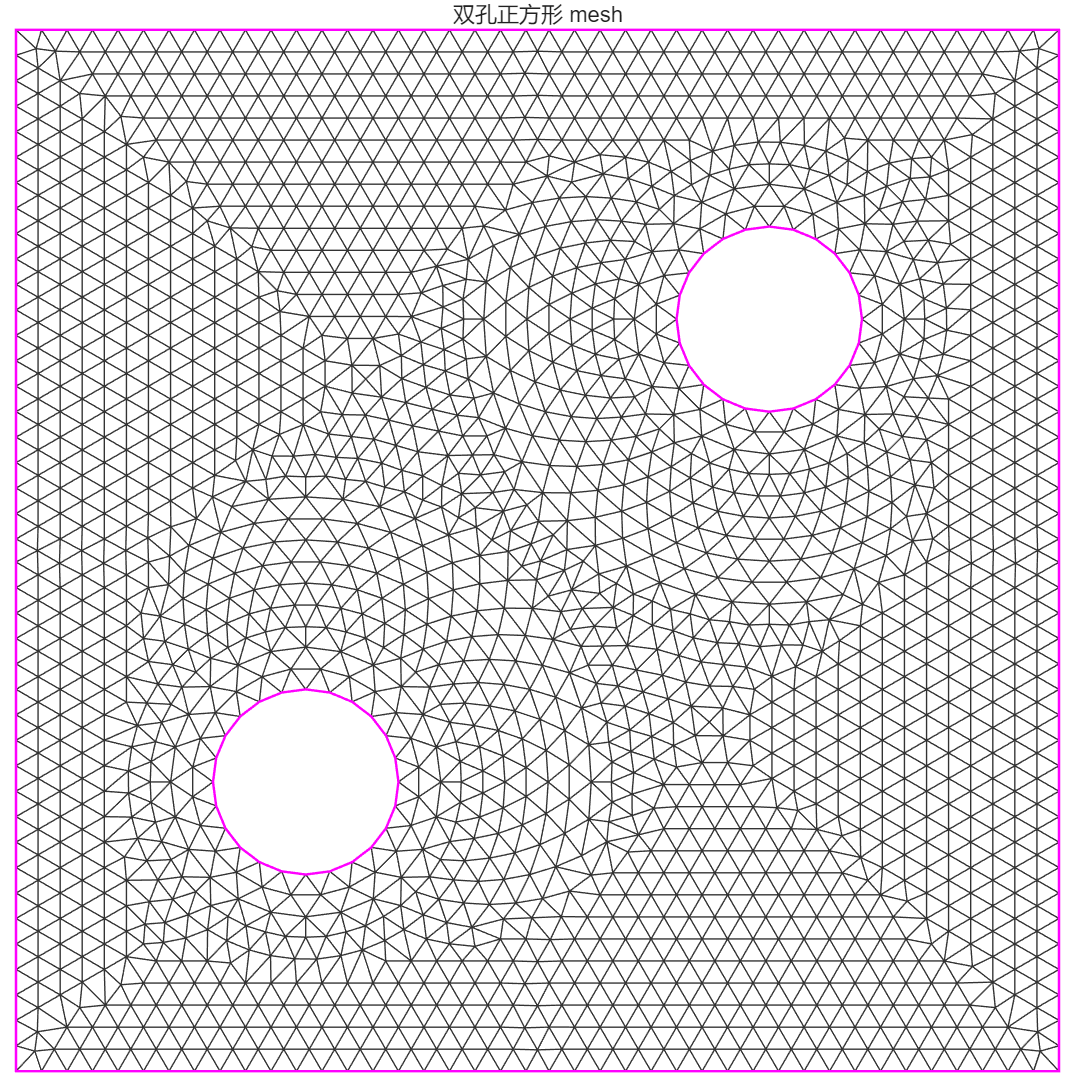
title('双孔正方形 mesh');