跳转至

Mesh2D : 密度函数的使用

约 1651 个字 196 行代码 14 张图片 预计阅读时间 8 分钟

本期内容向大家介绍非结构网格划分时很重要的概念— 网格密度函数。

主要内容包括：

  1. 网格密度函数的重要性
  2. Mesh2D 项目中如何定义网格密度函数
  3. 网格密度函数的理解（个人看法）
  4. 实际案例

重要性

无论是 2D 项目还是 3D 项目，网格密度控制都是至关重要的一个环节。现实工程中，一个较为复杂的模型不可能整体网格都是非常精细的，这样会极大地浪费计算资源并增加计算负担。因此，对感兴趣区域进行局部网格加密，既保证了仿真结果的准确性，也能极大提升计算效率。这也是每一位 CAE 工程师在网格划分阶段需要关注的重点。

在学习一些优秀的开源非结构网格划分程序时，我们会发现 网格密度函数 的思想被广泛采用。比如：

  1. DistMesh：基于距离函数和密度函数的自适应三角网格生成工具，可以通过自定义密度函数在特定区域加密网格
  2. Gmsh：功能强大的三维有限元网格生成器，支持通过背景场（Background Field）定义空间变密度，灵活地控制网格的局部细化
  3. Triangle：著名的二维三角网格生成器，通过区域密度约束函数对网格进行加密，常用于有限元和计算流体力学仿真
  4. TetGen：三维四面体网格生成工具，支持通过点密度函数控制局部网格大小，常用于医学建模和工程仿真
  5. Netgen：支持复杂几何体的三维网格剖分，可通过“网格大小函数”自适应细化特定区域

这些程序大多支持用户自定义密度函数或者背景场，从而让用户可以在物理特征复杂、几何细节丰富的区域生成更精细的网格，而在无关紧要的区域保持较粗的网格分布，实现仿真精度与效率的平衡。

Mesh2D 中的网格密度函数

Mesh2D支持任意用户自定义 mesh-size 函数 hfun，从而实现局部加密、梯度过渡、物理场驱动等复杂 mesh-size 分布控制。

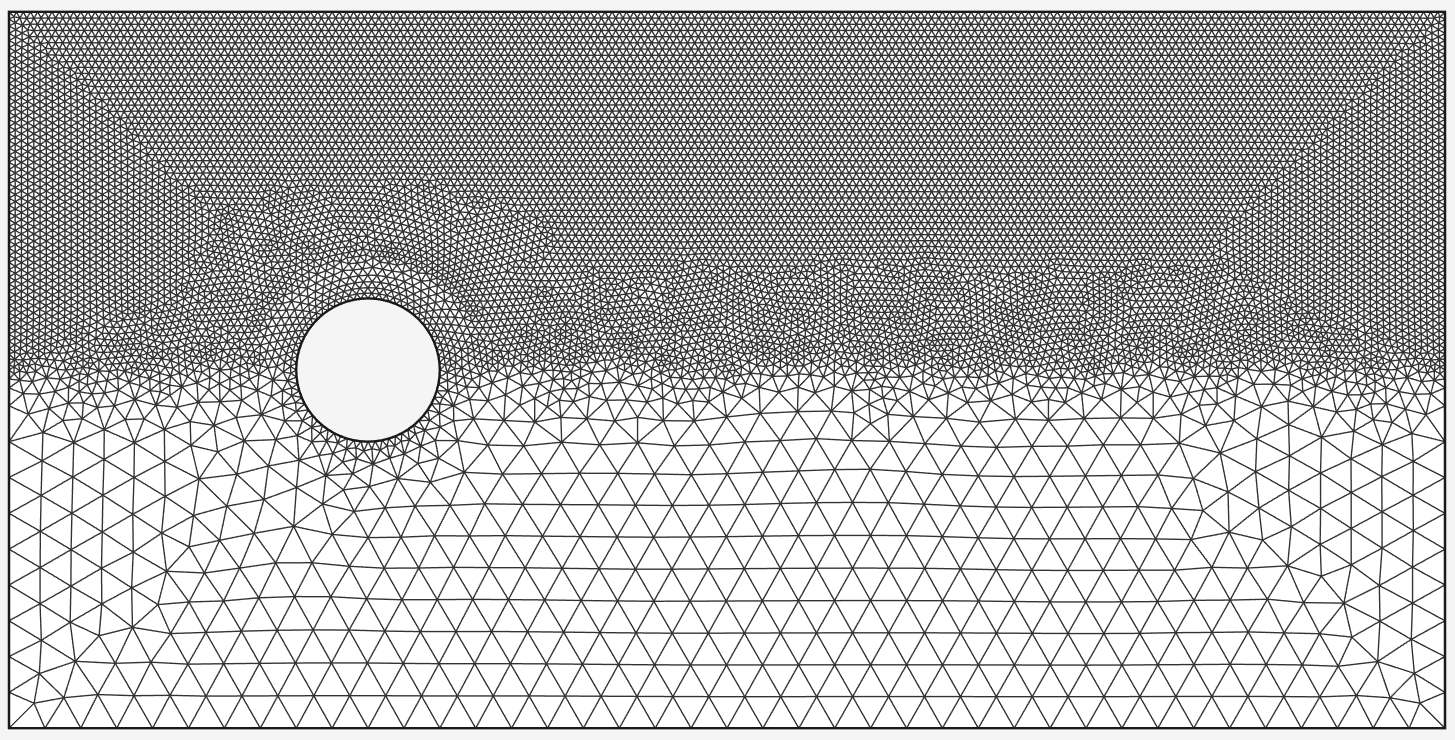
可以看到下面的网格分布图，矩形板内部有一个圆孔区域，围绕圆孔周围进行局部加密网格单元，加密的方式是我们自定义的“密度场”。

基础设置

定义几何区域

node = [
    -1, -1; +3, -1;
    +3, +1; -1, +1
];
edge = [
    1, 2; 2, 3; 3, 4; 4, 1
];
N_circ = 64;
theta = linspace(0, 2*pi, N_circ+1)'; theta(end) = [];
xcir = 0.20 * cos(theta);
ycir = 0.20 * sin(theta);
ncir = [xcir, ycir];
ecir = [(1:N_circ)', [2:N_circ,1]'];
ecir = ecir + size(node,1);

node = [node; ncir];
edge = [edge; ecir];

自定义网格密度函数

hfun = @hfun8;

其中hfun8：

function hfun = hfun8(xy)
% xy: N x 2
% 返回每个点的 mesh-size（可自由编写各类物理/几何控制）
    hmax = 0.05; % 最粗
    hmin = 0.01; % 最密
    xmid = 0.0;  % 加密中心
    ymid = 0.0;
    % 指数型衰减：离圆心越近，越密
    hcir = exp( -0.5*(xy(:,1)-xmid).^2 - 2.0*(xy(:,2)-ymid).^2 );
    hfun = hmax - (hmax-hmin)*hcir;
end

网格优化

[vert, etri, tria, tnum] = refine2(node, edge, [], [], hfun);
[vert, etri, tria, tnum] = smooth2(vert, etri, tria, tnum);

可视化

figure;
patch('faces',tria(:,1:3),'vertices',vert, ...
      'facecolor','w','edgecolor',[.2,.2,.2],'facealpha',0.96);
hold on; axis image off;
patch('faces',edge(:,1:2),'vertices',node, ...
      'edgecolor',[.1,.1,.1],'linewidth',1.2);
title('自定义 mesh-size 函数分布下的 mesh2d 网格');

% 显示 mesh-size field
figure;
patch('faces',tria(:,1:3),'vertices',vert, ...
      'facevertexcdata',hfun(vert), ...
      'facecolor','interp','edgecolor','none');
hold on; axis image off;
title('自定义 mesh-size field 可视化');
colorbar;

网格密度函数（个人理解）

几何区域内每个点的网格尺寸，称为mesh-size field，现设计一个函数：

\[ h ( x , y ) : \Omega \to ( 0 , + \infty ) \]

其中 \(\Omega\) 是几何域，\(h(x,y)\) 在每个点给出“希望的三角形边长”。mesh2d 可以自动在空间中布点，使得 绝大多数生成的三角形的边长大约为 \(h(x,y)\) 的数值。

可以理解为 非均匀网格布点的密度控制函数，控制着每一小块区域内的 mesh 点间距。小的 \(h(x,y)\)：网格更密，节点更多，单元更小；大的 \(h(x,y)\)：网格更稀疏，节点更少，单元更大。

接下来以几个直观的例子，来感受hfun。

实际案例

分段多区

比如想让 \(y>0\) 区域单元尺寸小一些，\(y<0\) 区域单元尺寸大一些。我们可以定义：

\[ h\left( x,y \right) =\begin{cases} 0.02,y>0\\ 0.1,y\leqslant 0\\ \end{cases} \]
function h = hfun8(xy)
    h = 0.1*ones(size(xy,1),1);
    h(xy(:,2) > 0) = 0.02;
end

网格划分效果：

中心加密，远区变粗

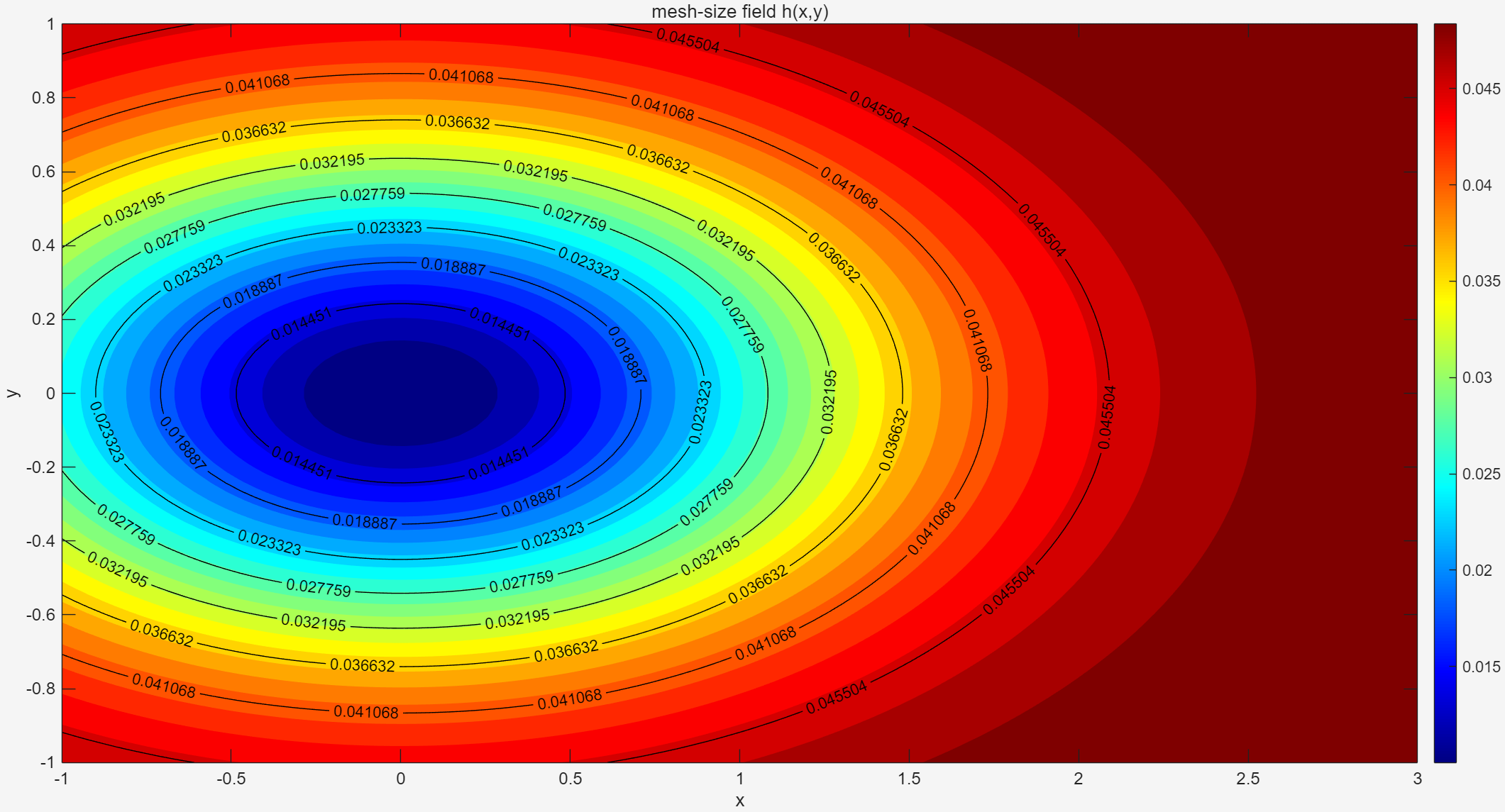
也就是本次 demo 的加密策略：

\[ h ( x , y ) = h _ { \mathrm { m a x } } - \left( h _ { \mathrm { m a x } } - h _ { \mathrm { m i n } } \right) \cdot \exp \left[ - 0 . 5 ( x - x _ { 0 } ) ^ { 2 } - 2 . 0 ( y - y _ { 0 } ) ^ { 2 } \right] \]
  • hmax=0.05：远离中心时的最大单元边长（网格最粗）
  • hmin⁡=0.01：在中心(x0,y0)处 mesh-size 最小（网格最密）
  • 指数衰减的两个系数 \(0.5\) 和 \(2.0\) 控制加密带的“椭圆形状”和衰减速度，\(y\) 方向加密区更窄更快网格更粗，\(x\) 方向更宽

可以绘制密度函数：

分段阶梯型（区内密、区外粗）

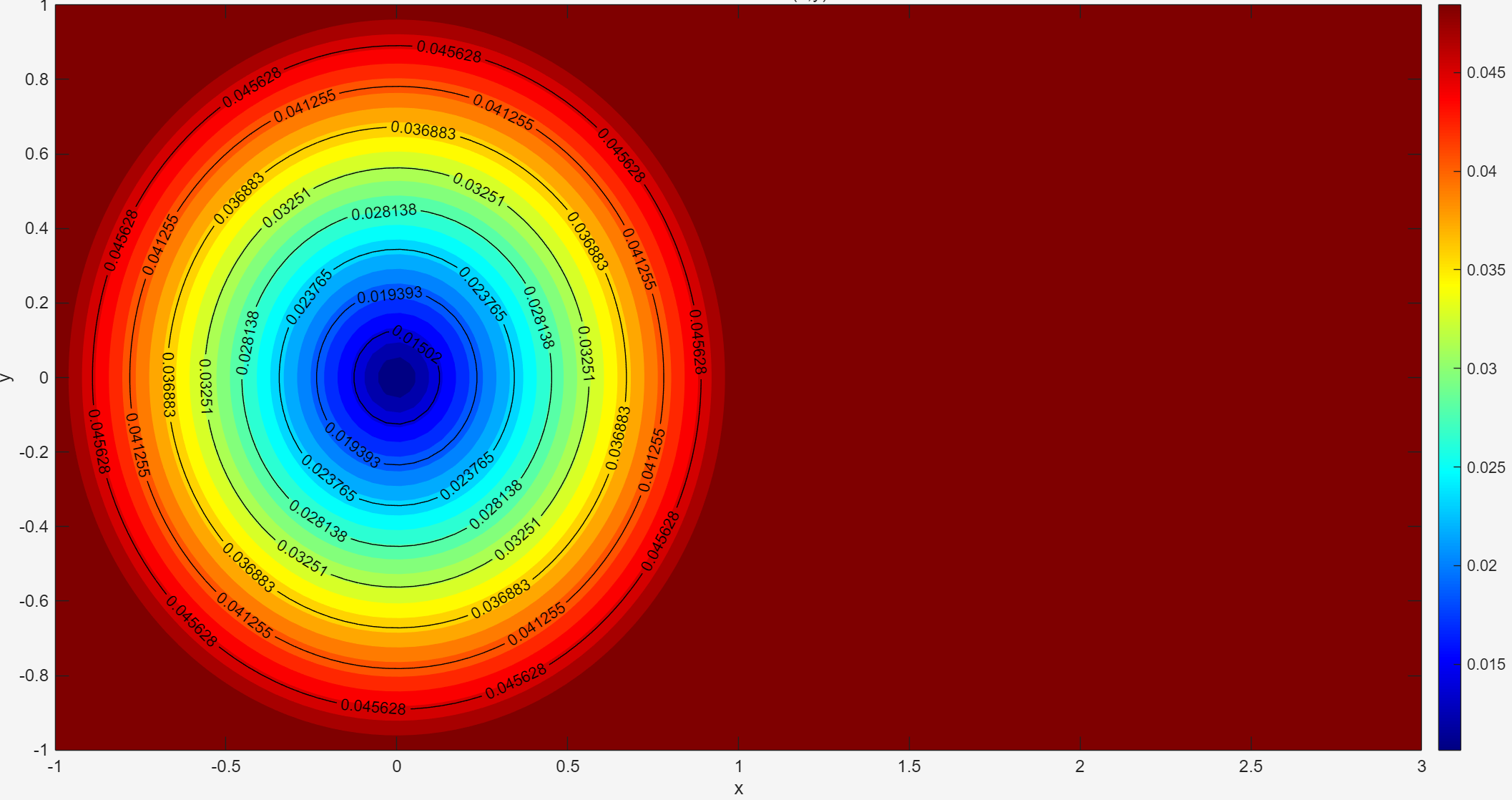
\[ h\left( x,y \right) =\begin{cases} h_{\min}，(x-x_0)^2+(y-y_0)^2 < r^2 \\ h_{\max},否则\\ \end{cases} \]
  • 中心圆内均匀细密，外部突然变粗
  • mesh2d 会自动在 孔边界附近 加一圈“额外的密集网格”，曲线边界附近 mesh2d 总会自动细化，以更好地贴合几何边界/保持质量
function h = hfun_step(xy)
    hmin = 0.01; hmax = 0.05;
    x0 = 0; y0 = 0; r = 0.5;
    r2 = (xy(:,1)-x0).^2 + (xy(:,2)-y0).^2;
    h = hmax*ones(size(xy,1),1);
    h(r2 < r^2) = hmin;
end

线性过渡型（径向线性变密）

\[ h ( x , y ) = h _ { \operatorname* { m i n } } + \left( h _ { \operatorname* { m a x } } - h _ { \operatorname* { m i n } } \right) \cdot \frac { r } { R } \]

其中，\(r = { \sqrt { ( x - x _ { 0 } ) ^ { 2 } + ( y - y _ { 0 } ) ^ { 2 } } }\)，\(R\) 为最大半径。

特点：中心最密，边缘线性变粗，过渡平滑、无突变。

function h = hfun_linear(xy)
    hmin = 0.01; hmax = 0.05;
    x0 = 0; y0 = 0; R = 1.0;
    r = sqrt((xy(:,1)-x0).^2 + (xy(:,2)-y0).^2);
    h = hmin + (hmax-hmin)*min(r/R, 1);
end

多圆加密型

\[ h(x,y)=\left\{ \begin{array}{l} h_{\min},在任意一个圆内\\ h_{\max}\text{，否则}\\ \end{array} \right. \]

特点：多个区域加密，其它区稀疏

function h = hfun_multi(xy)
    hmin = 0.01; hmax = 0.06;
    centers = [0 0; 0.7 0.5; -0.6 -0.3];
    r0 = 0.32;
    h = hmax*ones(size(xy,1),1);
    for k = 1:size(centers,1)
        r2 = (xy(:,1)-centers(k,1)).^2 + (xy(:,2)-centers(k,2)).^2;
        h(r2 < r0^2) = hmin;
    end
end

椭圆型/条带型加密（如裂缝或界面带状区）

\[ h(x,y)=\left\{ \begin{array}{l} h_{\min},\quad (\frac{x-x_0}{a})^2+(\frac{y-y_0}{b})^2<1\\ h_{\max}\text{，否则}\\ \end{array} \right. \]

特点：条带状区域密，其它区粗

function h = hfun_ellipse(xy)
    hmin = 0.01; hmax = 0.05;
    x0 = 0.5; y0 = 0;
    a = 0.6; b = 0.18;
    ell = ((xy(:,1)-x0)/a).^2 + ((xy(:,2)-y0)/b).^2;
    h = hmax*ones(size(xy,1),1);
    h(ell < 1) = hmin;
end

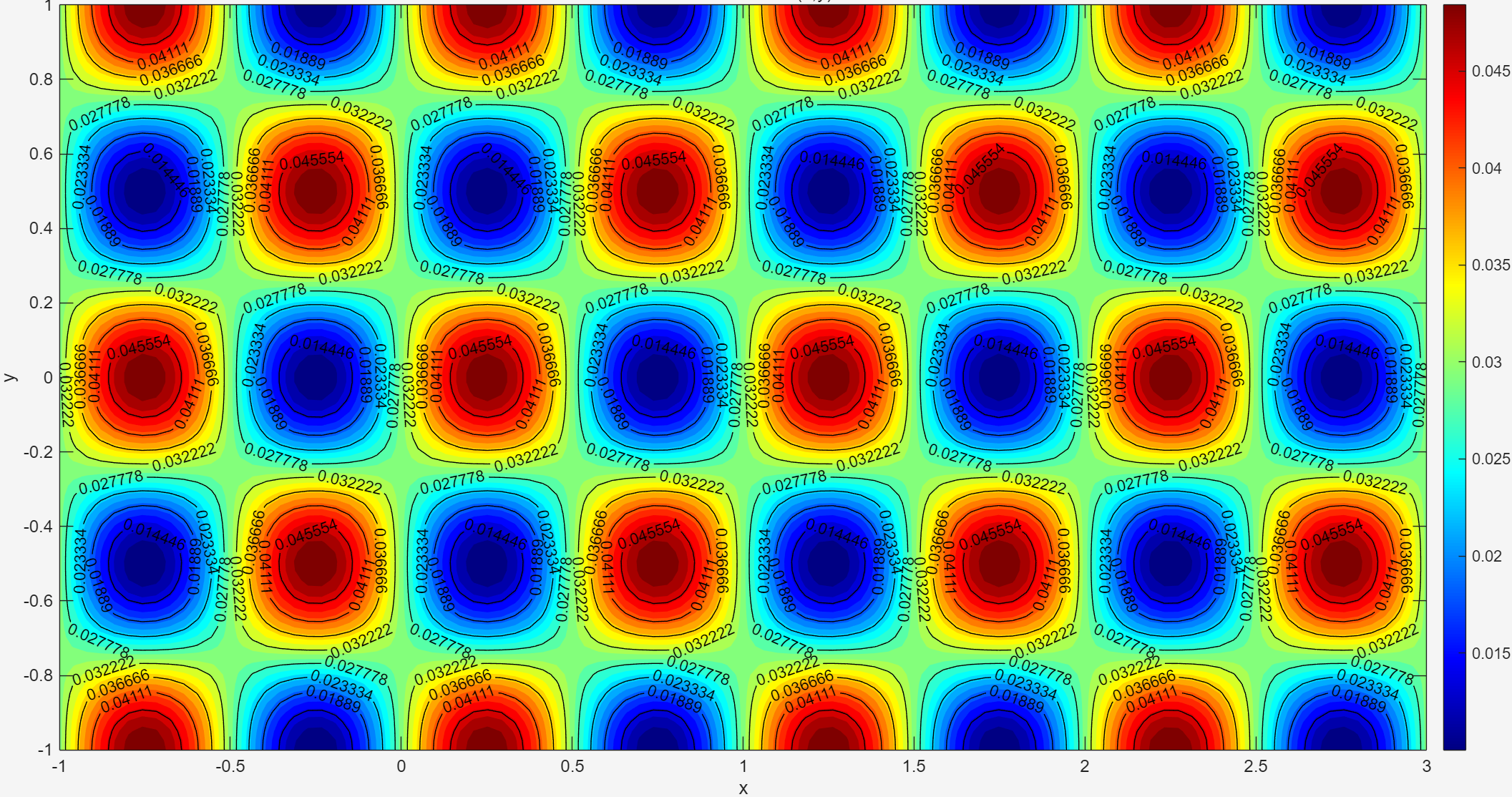
二维正弦型周期加密

\[ h ( x , y ) = h _ { \mathrm { m i n } } + \left( h _ { \mathrm { m a x } } - h _ { \mathrm { m i n } } \right) \cdot \frac { 1 + \sin ( 2 \pi x ) \cos ( 2 \pi y ) } { 2 } \]
function h = hfun_wave(xy)
    hmin = 0.01; hmax = 0.05;
    h = hmin + (hmax-hmin)*(1 + sin(2*pi*xy(:,1)).*cos(2*pi*xy(:,2)))/2;
end

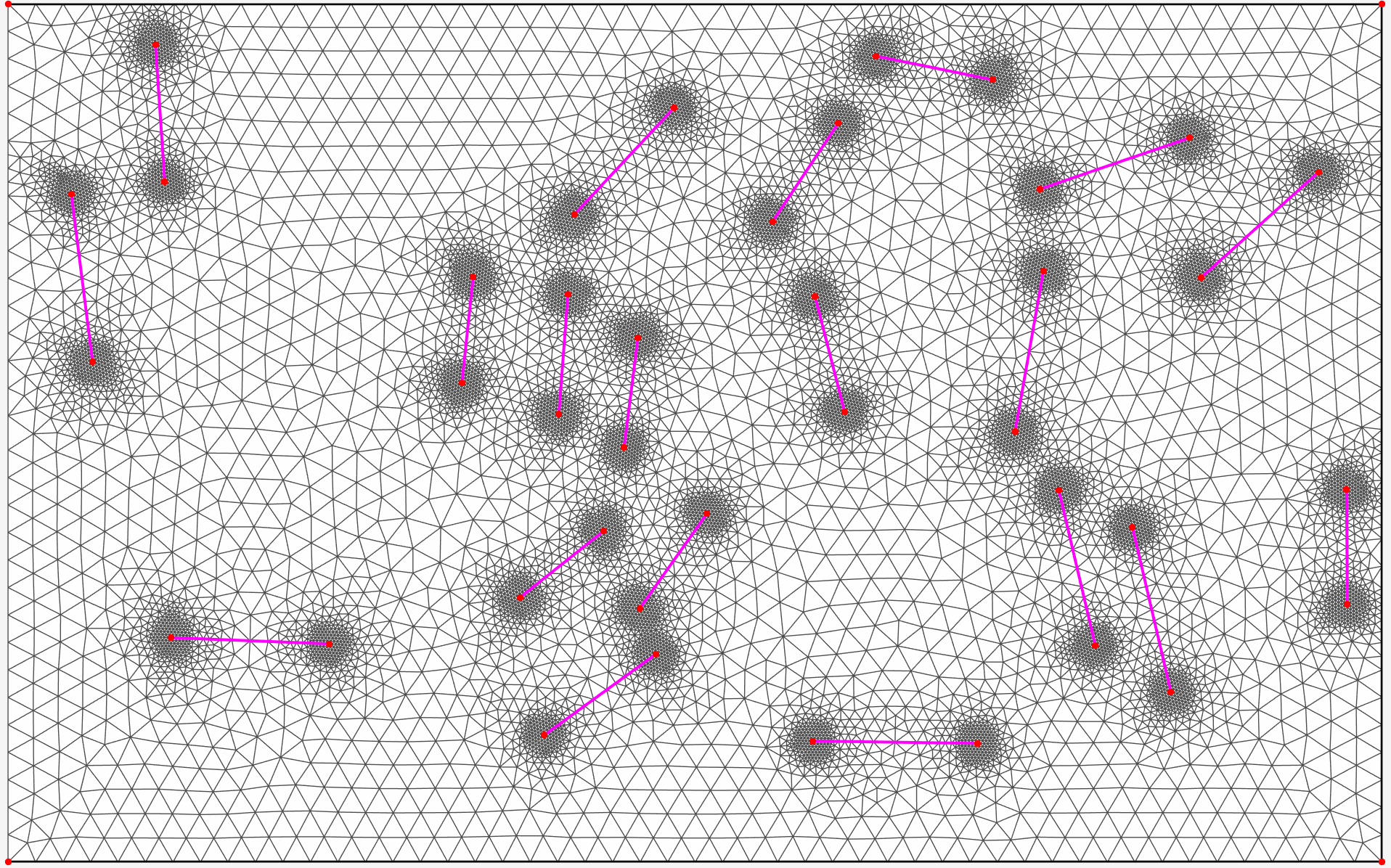
随机裂纹附近加密

设纤维/裂纹由线段 \([A_{K},B_{k}]\) 构成，定义每个点到所有纤维的最近距离 \(d(x,y)\)。

\[ h(x,y)=\left\{ \begin{array}{l} h_{\min},& d(x,y) < w_1\\ h_{\min}+(h_{\max}-h_{\min})\frac{d(x,y)-w_1}{w_2-w_1},& w_1\le d(x,y) < w_2\\ h_{\max},& d(x,y)\ge w_2\\ \end{array} \right. \]

其中 \(w_1\) 为最密带宽，\(w_2\) 为加密影响宽，可以修改 \(w_{1}\) 和 \(w_{2}\) 来控制网格加密情况。

在 demo6（后续有相关推文介绍） 的网格划分位置修改为：

hfun = @(xy) hfun8(xy, fiber_pts, fiber_edges);
[vert, etri, tria, tnum] = refine2(node, edge, part, [], hfun);
[vert, etri, tria, tnum] = smooth2(vert, etri, tria, tnum);

其中hfun8为：

function h = hfun8(xy, fiber_pts, fiber_edges)
    hmin = 0.01;  % 裂纹最密
    hmax = 0.08;  % 背景最粗
    w1 = 0.04;    % 最密带宽度
    w2 = 0.14;    % 加密带宽

    d = min_dist_to_fibers(xy, fiber_pts, fiber_edges);

    h = hmax*ones(size(xy,1),1);
    h(d < w2) = hmin + (hmax-hmin)*(d(d < w2) - w1)/(w2-w1);
    h(d < w1) = hmin;
    h(h < hmin) = hmin; % 限制下界
    h(h > hmax) = hmax; % 限制上界
end

function d = min_dist_to_fibers(xy, fiber_pts, fiber_edges)
    % xy: N x 2, fiber_pts: M x 2, fiber_edges: K x 2
    N = size(xy,1); K = size(fiber_edges,1);
    d = inf(N,1);
    for i = 1:K
        p1 = fiber_pts(fiber_edges(i,1),:);
        p2 = fiber_pts(fiber_edges(i,2),:);
        v = p2 - p1;
        len2 = sum(v.^2);
        w = bsxfun(@minus, xy, p1);
        t = max(0, min(1, sum(w.*v,2)/len2));
        proj = p1 + t.*v;
        dist = sqrt(sum((xy - proj).^2,2));
        d = min(d, dist);
    end
end

随机裂纹裂尖区域局部加密

需要 计算每个点与所有裂尖（端点）的距离，然后 只在这些端点附近设置 mesh-size 取最小值，其余区域正常（用较大 mesh-size）。

其中:

  • \(d_{tip}(x,y)\) 表示点到所有裂尖端点的最近距离
  • \(r_{1}\) 为加密核心半径，\(r_2\) 为加密带宽

假设裂纹/纤维端点集合为tip_pts，维度 \(N_{tip}\times 2\)：

function d = min_dist_to_tips(xy, tip_pts)
    % xy: N x 2, tip_pts: K x 2
    N = size(xy,1); K = size(tip_pts,1);
    d = inf(N,1);
    for i = 1:K
        d = min(d, sqrt(sum((xy - tip_pts(i,:)).^2, 2)));
    end
end

function h = hfun_tip(xy, tip_pts)
    hmin = 0.01;   % 裂尖最密
    hmax = 0.08;   % 其余区域最大
    r1 = 0.06;     % 最密核心半径
    r2 = 0.15;     % 加密带宽

    d = min_dist_to_tips(xy, tip_pts);

    h = hmax*ones(size(xy,1),1);
    idx1 = (d < r1);
    idx2 = (d >= r1) & (d < r2);
    h(idx1) = hmin;
    h(idx2) = hmin + (hmax-hmin)*(d(idx2)-r1)/(r2-r1);
end

在 demo6（后续有相关推文介绍）的网格划分位置修改为：

tip_pts = fiber_pts(fiber_edges(:), :); % 获取裂尖端点
hfun = @(xy) hfun8(xy, tip_pts);
[vert, etri, tria, tnum] = refine2(node, edge, part, [], hfun);
[vert, etri, tria, tnum] = smooth2(vert, etri, tria, tnum);

随机骨料模型局部加密

\[ h(x,y)=\left\{ \begin{array}{c} \begin{array}{l} h_{\mathrm{fine}},& \,\text{若离细骨料圆边界} < w_1\\ h_{\mathrm{medium​}},& \text{若离细骨料圆边界} < w_1\\ h_{\mathrm{coarse}},& \text{若离细骨料圆边界} < w_1\\ \end{array}\\ h_{\mathrm{sand}}, \text{否则}\\ \end{array} \right. \]

对于每个点 \((x,y)\)：

  1. 所有细骨料圆边界的最近距离 \(d_{min}^{(1)}\)
  2. 所有中骨料圆边界的最近距离 \(d_{min}^{(2)}\)
  3. 所有粗骨料圆边界的最近距离 \(d_{min}^{(3)}\) 
function h = hfun8(xy, agg_xy, agg_r, agg_type)
    % xy: N x 2
    % agg_xy: M x 2, agg_r: M x 1, agg_type: M x 1 (1=细,2=中,3=粗)
    % 自定义各类 mesh-size
    h_sand   = 0.15;
    h_fine   = 0.015;
    h_medium = 0.03;
    h_coarse = 0.05;
    % 各类加密带宽（距离骨料边界的带宽）
    w_fine   = 0.07;
    w_medium = 0.09;
    w_coarse = 0.11;

    N = size(xy,1);
    h = h_sand*ones(N,1); % 默认基体密度

    % 针对细骨料
    idx = (agg_type == 1);
    if any(idx)
        d_fine = min_dist_to_circles(xy, agg_xy(idx,:), agg_r(idx));
        h(d_fine < w_fine) = h_fine;
    end

    % 针对中骨料
    idx = (agg_type == 2);
    if any(idx)
        d_med = min_dist_to_circles(xy, agg_xy(idx,:), agg_r(idx));
        mask = (d_med < w_medium) & (h > h_medium);
        h(mask) = h_medium;
    end

    % 针对粗骨料
    idx = (agg_type == 3);
    if any(idx)
        d_coarse = min_dist_to_circles(xy, agg_xy(idx,:), agg_r(idx));
        mask = (d_coarse < w_coarse) & (h > h_coarse);
        h(mask) = h_coarse;
    end
end

function d = min_dist_to_circles(xy, centers, radii)
    % 计算每个点到所有圆边界的最小距离（可正可负）
    N = size(xy,1); K = size(centers,1);
    d = inf(N,1);
    for i = 1:K
        dist_center = sqrt(sum((xy - centers(i,:)).^2, 2));
        d = min(d, abs(dist_center - radii(i)));  % 圆边界绝对距离
    end
end

参数调节：

  • h_fine, h_medium, h_coarse, h_sand — 分别控制细/中/粗骨料/基体 mesh-size
  • w_fine，w_medium — 控制骨料附近“加密影响区”的宽度
  • 可以把加密带宽设宽点/密度差拉大/缩小，效果对比更明显。

随机骨料+钢纤维模型局部加密

将上面两个例子结合来做：