三维Timoshenko梁单元

单元描述

局部坐标系下的梁单元每个节点具有 6 个自由度，

上图所示的空间梁单元节点位移列向量 $\mathbf{q}^e$ 和节点力列向量 $\mathbf{P}^e$ 分别为:

$$\mathbf{q}_{(12\times1)}^e=\begin{bmatrix}u_1&\nu_1&w_1&\theta_{x1}&\theta_{y1}&\theta_{z1}&u_2&\nu_2&w_2&\theta_{x2}&\theta_{y2}&\theta_{z2}\end{bmatrix}^T$$

$$\mathbf{P}_{(12\times1)}^e=\begin{bmatrix}P_{u1}&P_{v1}&P_{w1}&M_{x1}&M_{y1}&M_{z1}&P_{u2}&P_{v2}&P_{w2}&M_{x2}&M_{y2}&M_{z2}\end{bmatrix}^T$$

相应的刚度方程为：

$$\mathbf{K}_{(12\times12)}^e\cdot\mathbf{q}_{(12\times1)}^e=\mathbf{P}_{(12\times1)}^e$$

单元刚度矩阵计算

与空间的 Euler-Bernoulli 梁单元刚度矩阵叠加类似，空间 Timoshenko 梁单元刚度矩阵为一个 $12\times 12$ 的矩阵，看似很麻烦，实则可以根据刚度矩阵叠加原则，一点一点叠加上去！

轴向刚度：轴向位移，对应于节点位移 $(u_1,u_2)$，直接应用杆单元的刚度矩阵：

$$\mathbf{K}^e=\frac{EA}{l}\begin{bmatrix}1&-1\\-1&1\end{bmatrix}$$

扭转刚度：扭转角，对应于节点位移 $(\theta_{x1},\theta_{x2})$

$$\mathbf{K}^e=\frac{GJ}{l}\begin{bmatrix}1&-1\\-1&1\end{bmatrix}$$

其中，$J$ 为横截面的扭转惯性矩，$G$ 为剪切模量。

纯弯刚度：对应于节点位移 $(\theta_{y1},\theta_{z1},\theta_{y2},\theta_{z2})$
对于 $(\theta_{y1},\theta_{y_{2}})$：

$$\mathbf{K}^e=\frac{EI_{y}}{l}\begin{bmatrix}1&-1\\-1&1\end{bmatrix}$$

对于 $(\theta_{z1},\theta_{z2})$：

$$\mathbf{K}^e=\frac{EI_{z}}{l}\begin{bmatrix}1&-1\\-1&1\end{bmatrix}$$

剪切刚度：对应于节点位移 $(v_{1},w_{1},\theta_{y1},\theta_{z1},v_{2},w_{2},\theta_{y2},\theta_{z2})$

对于 $(v_{1},\theta_{y1},v_{2},\theta_{y2})$

$$\mathbf{K}^e = {\color{red} f_{py}^{\alpha}}\frac{GA}{4kl} \begin{bmatrix} 4 & 2l & -4 & 2l \\ 2l & l^2 & -2l & l^2 \\ -4 & -2l & 4 & -2l \\ 2l & l^2 & -2l & l^2 \end{bmatrix}$$

其中，

$$f_{py}^{\alpha} = 1/\left(1+\xi^*SCF\frac{l^2A}{12I_{y}}\right)$$

对于 $(w_{1},\theta_{z1},w_{2},\theta_{z2})$

$$\mathbf{K}^e = {\color{red} f_{pz}^{\alpha}}\frac{GA}{4kl} \begin{bmatrix} 4 & 2l & -4 & 2l \\ 2l & l^2 & -2l & l^2 \\ -4 & -2l & 4 & -2l \\ 2l & l^2 & -2l & l^2 \end{bmatrix}$$

其中，

$$f_{pz}^{\alpha} = 1/\left(1+\xi^*SCF\frac{l^2A}{12I_{z}}\right)$$

剪切刚度矩阵修正

对于上面公式中出现的 $f_{p}^{\alpha}$ ，是 Abaqus 内部对于剪切刚度矩阵的修正方式，为了对标Abaqus，可以仿照Abaqus对剪切部分的刚度矩阵进行修正，相关理论可点击查看：Abaqus 官方文档

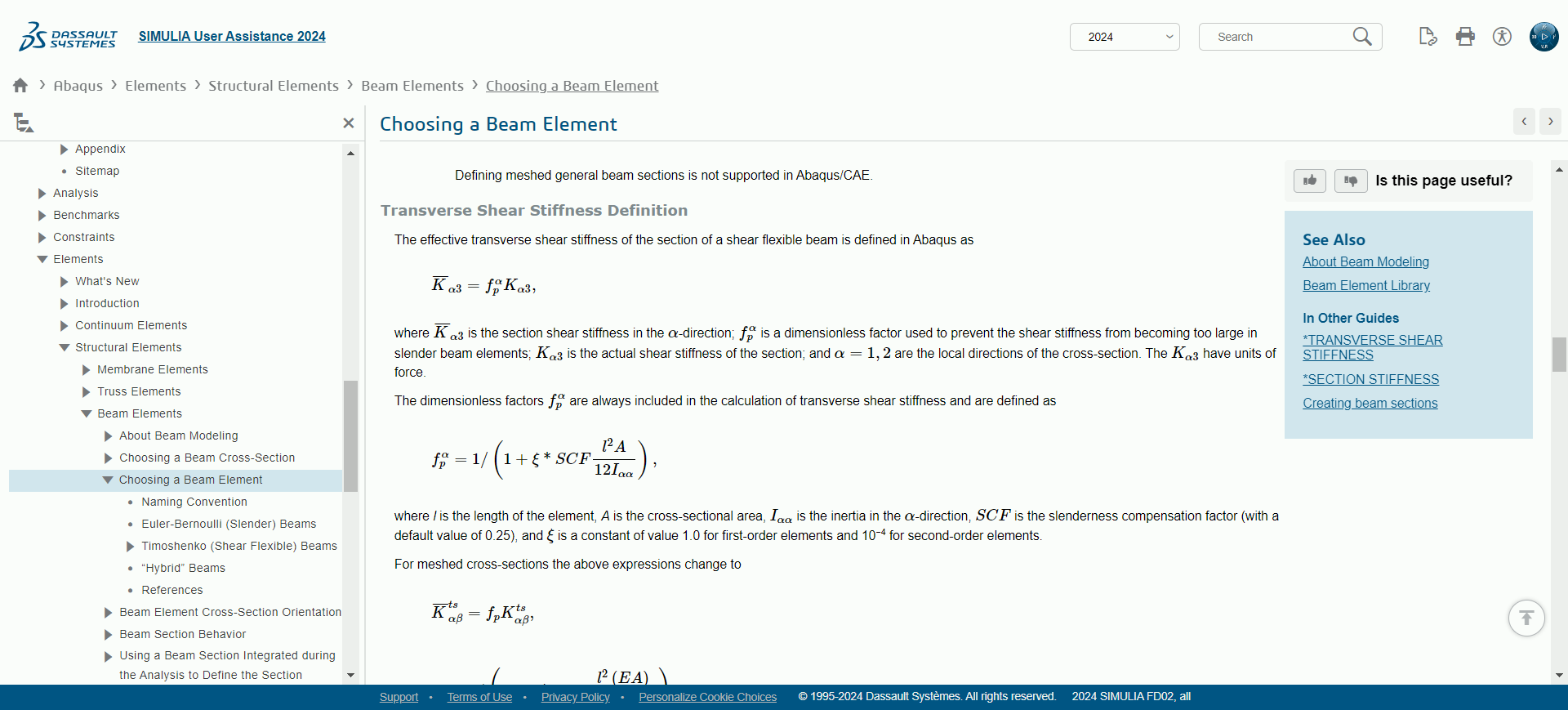
具体啥意思呢？我来自己总结下，不一定对，仅供参考哈！

$$\overline{K}_{\alpha3}=f_p^\alpha K_{\alpha3}$$

其中，$\overline{K}_{\alpha3}$ 表示修正后的剪切刚度矩阵，$K_{\alpha3}$ 表示未被修正的剪切刚度矩阵，$f_p^\alpha$ 表示的是一个无量纲因子，预防梁的剪切刚度过大。

$$f_p^\alpha=1/\left(1+\xi^*SCF\frac{l^2A}{12I_{\alpha\alpha}}\right)$$

其中，$A$ 表示截面面积，对于一阶单元 $\xi$ 为 1.0，对于二阶单元 $\xi$ 为 $10^{-4}$，SCF默认值为0.25，$I_{\alpha\alpha}$ 为截面惯性矩，$l$ 为梁长。

---

最终叠加后的单元刚度矩阵为:

$$\mathbf{K}^e=\left[ \begin{matrix} \frac{EA}{l}& 0& 0& 0& 0& 0& -\frac{EA}{l}& 0& 0& 0& 0& 0\\ 0& \frac{GA}{kl}& 0& 0& 0& \frac{GA}{2k}& 0& -\frac{GA}{kl}& 0& 0& 0& \frac{GA}{2k}\\ 0& 0& \frac{GA}{kl}& 0& -\frac{GA}{2k}& 0& 0& 0& -\frac{GA}{kl}& 0& -\frac{GA}{2k}& 0\\ 0& 0& 0& \frac{GJ}{l}& 0& 0& 0& 0& 0& -\frac{GJ}{l}& 0& 0\\ 0& 0& -\frac{GA}{2k}& 0& \frac{GAl}{4k}+\frac{EI_y}{l}& 0& 0& 0& \frac{GA}{2k}& 0& \frac{GAl}{4k}-\frac{EI_y}{l}& 0\\ 0& \frac{GA}{2k}& 0& 0& 0& \frac{GAl}{4k}+\frac{EI_z}{l}& 0& -\frac{GA}{2k}& 0& 0& 0& \frac{GAl}{4k}-\frac{EI_z}{l}\\ -\frac{EA}{l}& 0& 0& 0& 0& 0& \frac{EA}{l}& 0& 0& 0& 0& 0\\ 0& -\frac{GA}{kl}& 0& 0& 0& -\frac{GA}{2k}& 0& \frac{GA}{kl}& 0& 0& 0& -\frac{GA}{2k}\\ 0& 0& -\frac{GA}{kl}& 0& \frac{GA}{2k}& 0& 0& 0& \frac{GA}{kl}& 0& -\frac{GA}{2k}& 0\\ 0& 0& 0& -\frac{GJ}{l}& 0& 0& 0& 0& 0& \frac{GJ}{l}& 0& 0\\ 0& 0& -\frac{GA}{2k}& 0& \frac{GAl}{4k}-\frac{EI_y}{l}& 0& 0& 0& -\frac{GA}{2k}& 0& \frac{GAl}{4k}+\frac{EI_y}{l}& 0\\ 0& \frac{GA}{2k}& 0& 0& 0& \frac{GAl}{4k}-\frac{EI_z}{l}& 0& -\frac{GA}{2k}& 0& 0& 0& \frac{GAl}{4k}+\frac{EI_z}{l}\\ \end{matrix} \right]$$

数值案例

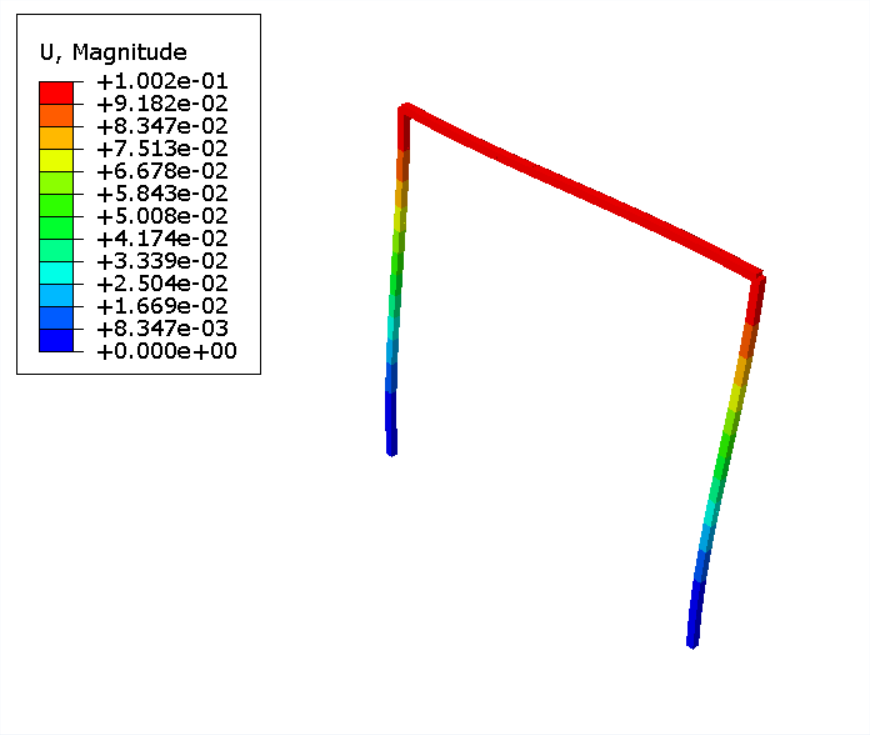
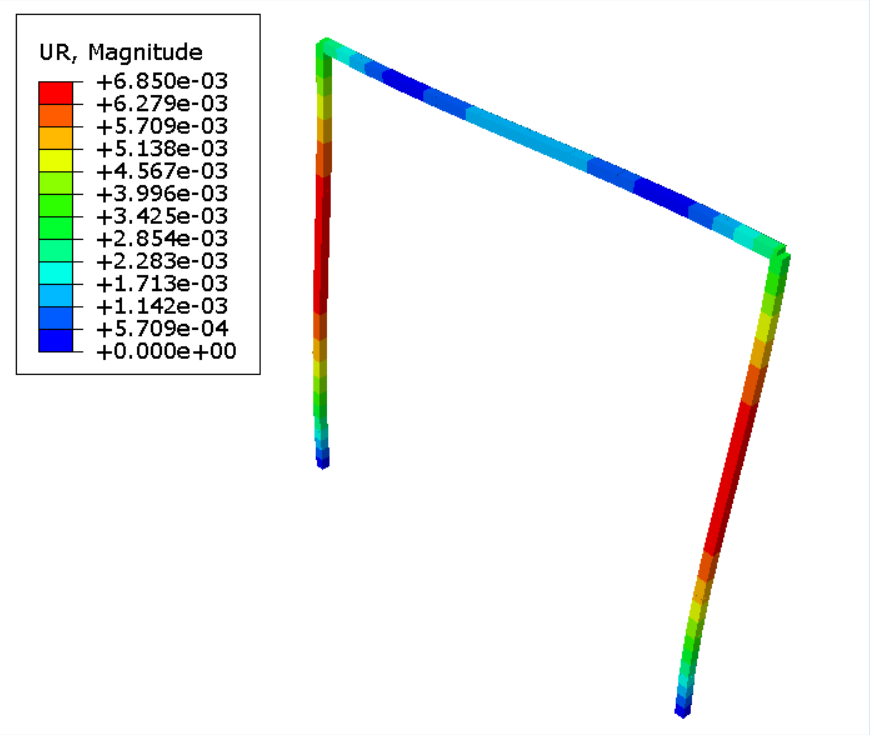
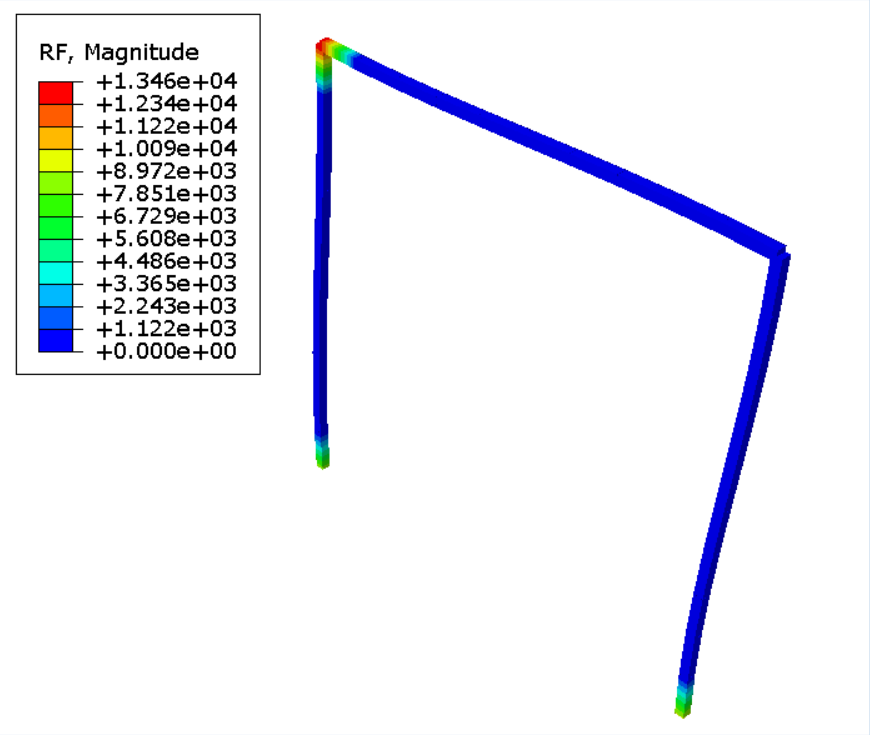
本次的案例将采用 Abaqus 对于 Timoshenko 梁剪切修正的方式进行数值编程，将单元刚度矩阵与 Abaqus 导出的单元刚度矩阵（以 1 号单元刚度矩阵为例）进行对标，位移场结果进行对标。几何模型及边界条件信息如下：

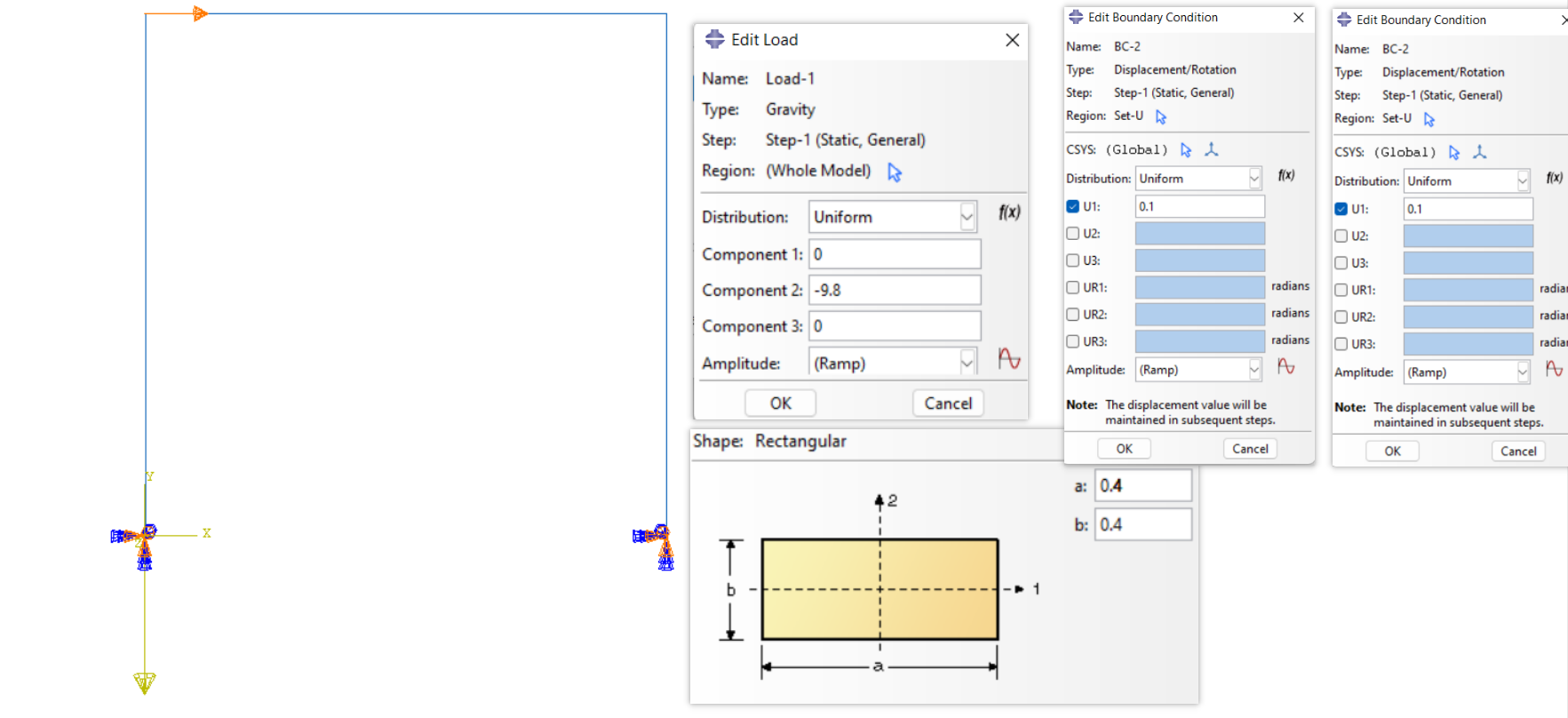
位移场对比

单元刚度矩阵对比

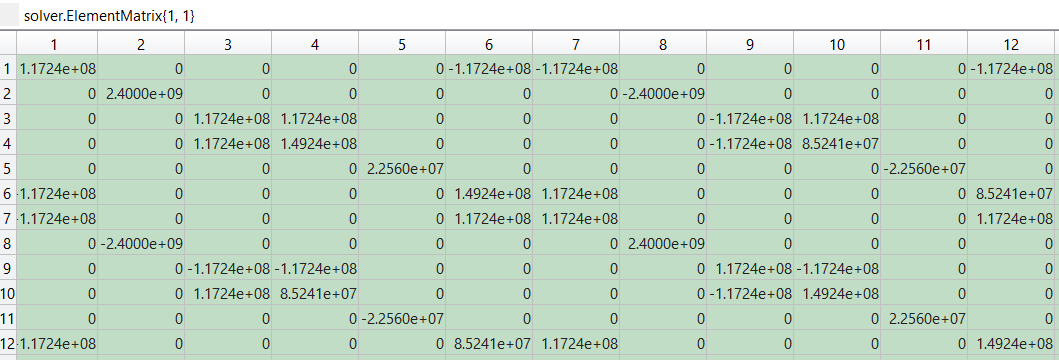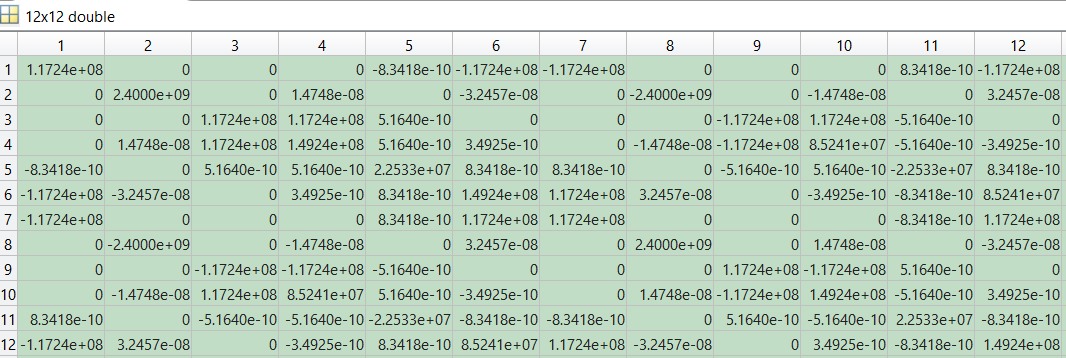MFEA 单元刚度矩阵	Abaqus 单元刚度矩阵

由以上对比结果可知，本次编制的三维 Timoshenko 梁单元刚度矩阵与 Abaqus 完全一致。